上一篇给大家推荐了学习"加法、乘法交换律及加法、乘法结合律"后，常出现的三种拓展变式题型。今天再向大家介绍两种：

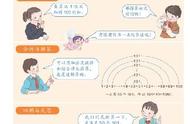
【高斯算法】因高斯最先灵活使用加法交换律和结合律算出"1 2 3 …97 98 99 100"而得名。

计算：1 2 3 … 98 99 100

方法一：①观察算式，运用加法交换律和结合律，可以发现，1 100，2 99，3 98，…50 51都分别得101；

②原算式共有100个加数，两两结合，可以得到50个101；

③原算式等于50×101，结果为5050。

1 2 3 …… 98 99 100

=（1 100） （2 99） … （50 51）

=101 101 … 101（共50个101）

=50×101

=5050

方法二：①观察算式可以发现，加数是连续的自然数1到100；

②根据加法交换律，算式"100 99 98 … 3 2 1"与原算式的和相等；

③把算式"1 2 3 …… 98 99 100"与算式"100 99 98 … 3 2 1"依次一一对应合并起来，正好是100个101；

④原式是其中的一半，结果是100×101后除以2，等于5050。

1 2 3 …… 98 99 100

=[（1 2 3 …… 98 99 100） （100 99 98 … 3 2 1）]÷2

=[（1 100） （2 99） … （100 1）] ÷2

=[101 101 … 101]÷2 （共100个101）

=101×100÷2

=5050

【等差数列求和】实质是高斯算法的进一步演化。因为四年级《运算定律》这单元学到的知识点较多，容易混淆的地方也较多，学生"观念转变，正确运用"基本定律需要较多的强化训练，所以在这里建议现阶段只要求学生掌握"等差数列"的特点及求和公式，项数的确定公式可以放到暑假再学习。

计算：2 4 6 … 16 18 20

方法：①观察算式可以发现，任意两个加数，后一个都比前一个多2，像这样"任意相邻的两个数的差都相等的"一组数，就叫等差数列；

②等差数列中"首项 末项"、"第二项 倒数第二项"、"第三项 倒数第三项"…和都相等，为什么？"2 20"、"4 18"、"6 16"…相邻两个算式比较，一项增加2，另一项正好减少了2；

③原算式共有10个加数（可以直接数出来，也可以想1-20共有20个，双数占一半，有10个），两两结合，可以得到（10÷2=5）个22；

④原算式等于（2 20）×10÷2，结果为110。

2 4 6 … 16 18 20

=（2 20）×10÷2

=110

等差数列求和公式：和=（首项 末项）×项数÷2

【练习】

①1＋2＋3＋4＋…＋78＋79＋80

②3＋6＋9＋12＋…＋1998＋2001

（是一组等差数列，项数的确定：关键在领会"2001是3的几倍，就有几项"）