一、由牛顿第二定律可知:合力F和加速度a具有瞬时对应关系1,因此对瞬时加速度问题分析的关键是对物体进行受力分析。我们可以采取“瞻前顾后”的方法,即既要分析运动状态变化前的受力,又要分析运动状态变化瞬间的受力,从而确定加速度。
二、在牛顿第二定律的应用中,瞬时加速度问题中常见力学模型有:①弹力可以发生突变的轻杆、轻绳、接触面;②极短时间内弹力来不及变化的弹簧和橡皮条。这两种力学模型在瞬时加速度问题中有以下特点(是分析问题的关键):
(1)轻绳、轻杆、接触面(木板、地面):它们都是一种不发生明显形变(发生微小形变)就能产生弹力的物体,若把一根拉紧的绳子剪断(或物体脱离轻杆、将木板抽出)后,其中的弹力就会立即发生变化,瞬间减少为0。
(2)弹簧、橡皮条:它们的特点都是容易发生形变、形变量大,恢复形变都需要比较长时间。在瞬时问题中,涉及到弹簧、橡皮条的弹力不变。
特别注意:对一般同学来说,在解决瞬时加速度问题时,特别是轻绳问题虽然懂得根据两种力学模型特点做出正确受力分析,但由于不知道加速度方向(合力方向)导致前功尽弃。瞬时加速度轻绳问题加速度(合力)方向:根据剪断瞬间物体做什么运动来确定,如剪断瞬间物体做圆周运动则瞬时加速度沿圆周的切线方向。
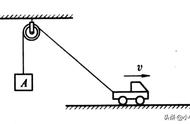
类型一、轻绳问题:加速度(合力)方向由物体运动确定。

类型二、弹簧问题:加速度(合力)方向直接根据前后受力分析比较确定。

类型三、轻杆(木板)问题:加速度(合力)方向直接根据前后受力分析比较确定。

类型四、连接体问题:连接体求瞬间加速度问题要根据两种力学模式特点进行隔离分析,最后由牛顿第二定律求出各自的瞬间加速度。

【试着做一做】

1.合力F和加速度a具有瞬时对应关系:F=ma对运动过程中的每一瞬间成立,某一时刻的加速度大小总跟那一时刻的合外力大小成正比,即有力的作用就有加速度产生。外力停止作用,加速度随即消失,在持续不断的恒定外力作用下,物体具有持续不断的恒定加速度。外力随着时间而改变,加速度就随着时间而改变。