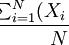方差也称为“平方差”，用来描述集合中变量的离散程度，即变量与平均值的偏离程度。方差越大，表示变量与平均值的偏离程度越大，即越不稳定。标准差是方差的算术平方根。今天这篇文章，我们就用SCL语言编写函数来计算方差和标准差。

统计学上方差分为两种：总体方差和样本方差。

①总体方差：是指总体中每一个变量与总体平均值的差值的平方和，除以总体数量。总体方差的计算公式如下：

其中：σ2是总体方差，X是随机变量，μ是总体均值，N是总体样本量。

实际情况中，我们可能得不到总体的所有变量，只能抽取有限数量的样本来代替整体，这种方差称为样本方差。

②样本方差：样本中所有变量与样本平均值的差值的平方和，除以样本数量（n-1）。样本方差的计算公式如下：

注意：样本方差中为了实现对总体的无偏估计，除数采用样本量减1。

③总体标准差：总体方差的算术平方根；

④样本标准差：样本方差的算术方法根；

接下来编程实现总体方差/标准差及样本方差/标准差的计算。

在博途环境下新建函数块FB5019_Variance，声明变量如下图所示：

其中：

• u2：总体方差；
• u：总体标准差；
• s2：样本方差；
• s：样本标准差；
• average：平均值；

编写代码如下：

我使用随机数产生函数测试过了这段代码，如果你有任何问题欢迎留言讨论。