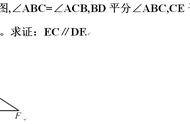相交线与平行线是平面几何图形中最为基础的一个环节，也是中招考试中的一个重要基础考点。题型相对简单，但灵活多变，需要掌握如下思想方法，则“万变不离其宗”。

类型1 方程思想

1.如图所示，l₁，l₂，l₃交于点O，∠1＝∠2，∠3∶∠1＝8∶1，则∠4的度数为 36°．

思路：往往设份数较小的量为x，表示出其他的量，列等量关系可得。

2.如图，已知直线AB、CD相交于O，OE⊥AB，垂足为O，OF平分∠AOC，∠AOF：∠AOD=5：26，则∠EOC的度数为 140° ．

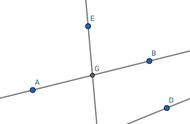
3.如图，由点O引出六条射线OA，OB，OC，OD，OE，OF，且AO⊥OB，OF平分∠BOC，OE平分∠AOD，若∠EOF＝170°，求∠COD的度数．

解：设∠COD＝x.因为OF平分∠BOC，OE平分∠AOD，

所以∠COF＝1/2∠BOC，∠EOD＝1/2∠AOD.

因为∠EOF＝x＋∠COF＋∠EOD＝170°，

所以∠COF＋∠EOD＝170°－x.

又因为x＋2∠COF＋2∠EOD＋90°＝360°，

所以x＋2(170°－x)＋90°＝360°，

所以x＝70°，即∠COD＝70°.

类型2 分类讨论思想（数形结合）

1. 已知∠α=80°，∠β的两边与∠α的两边分别垂直，则∠β=80°或100°

思路：通常与数形结合思想并用，发现遗漏的点，进而综合考虑，全面解决。

5.在同一平面内，三条直线的交点个数是0或1或2或3

6.在直线AB上任取一点O，过点O作射线OC，OD，使OC⊥OD，当∠AOC＝30°时，∠BOD的度数是多少？

解：如图①，当OC，OD在AB同侧时，

因为OC⊥OD，所以∠COD＝90°.

因为∠AOC＝30°，

所以∠BOD＝180°－∠COD－∠AOC＝60°.