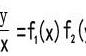本文主要内容，介绍利用下图所示微分方程通解方法求解二阶微分方程y" y=6(sinx)^2的通解。

该微分方程的特征方程为：

r^2 1=0

r^2=-1

r=±i

则其y" y=0的通解y*为：

y*=c1cosx c2sinx.

由于P（x）=6(sinx)^2，化简得到：

P(x)=3-3cos2x，分两种情况：

当p1(x)=3，此时可设特解y1=a.

代入微分方程得到：

0 a=3，即a=3，所以y1=3.

当p2(x)=-3cos2x，此时可设特解y2为：

y2=acos2x bsin2x.

y2’=-2asin2x 2bcos2x

y2"=-4acos2x-4bsin2x,则：

-3acos2x-3bsin2x =-3cos2x

所以a=1,b=0.

即：y2=cos2x

根据微分方程的通解与特解关系，

则此方程的通解为：

y=y* y1 y2

= c1cosx c2sinx 3 cos2x

=c1cosx c2sinx cos2x 3.