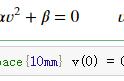（5）全微分方程：若存在二元函数u(x,y)，使du(x,y)=P(x,y)dx Q(x,y)dy，则称微分方程

P（x,y)dx Q（x,y)dy=0为全微分方程，它的通解为u(x,y)=C.

从上述总结的一阶微分方程的种类及解法可以看出，这类题目的题型多变，同学们需要强化记忆理解相关概念，注意区分，对不同类型的题目采取相对应的解法。

（6）可降阶的高阶微分方程

题型一：可降阶且不显y的微分方程

例1：（2007年考研真题)

分析：本题是可降阶且不显y的微分方程，可以通过令p=y'，把原方程化解程一阶线性微分方程。

解：