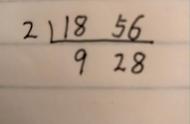一．概念描述

现代数学：最大公因数亦称最大公约数，是一种特殊的公因数。设a1，a2，...，an是n个整数(n≥2)，其公因数中最大的d称为a1，a2，...，an的最大公因数。最大公因数通常用圆括号表示，记为d=(a1，a2，...，an)。最大公因数有以下性质：

①a1，a2，...，an的最大公因数，是这组数的其他公因数的倍数。

②(a1，a2，...，an)=(a1，a2，...，an-1),an)。

③存在整数s，t，使得(a，b)=as bt成立。

④如果a，b都是大于1的正整数，它们的标准分解式分别为a=P^α1₁P^α2₂...P^αs_s，b=P^β1₁P^β2₂...P^βs_s。式中P₁<p₂<…<p_s是素数，αi，βi(i=1,2,...s)为非负整数，则(a,b)=p^e1₁p^e2₂...p^es_s。式中ei=min(αi，βi)(i=1,2,...s)。这个性质可以推广到有限个正整数的最大公因数的

情形。

⑤等式（a kb，b）=（a，b）对于任何整数a，b，k成立。

小学数学：小学数学教材中没有明确给出最大公因数的定义，重点是结合生活情境，帮助学生理解最大公因数的现实意义，并引导学生在充分认识公因数的基础上，体会最大公因数是指一组正整数公因数中最大的一个。（小学阶段在正整数范围内研究，不包括0。）

二．概念解读

最大公因数的上位概念是公因数。一般在教学中，公因数和最大公因数是同时进行研究的。之所以说它是一种特殊的公因数，其特殊性在于它在一组正整数的所有公因数中最大，所以称为最大公因数。

最大公因数与约分也有着密切的联系。如果用这个分数化简成最简分数时，需要进行约分。在约分的过程中，如果用这个分数的分子、分母的最大公因数去除，一次就可以将其化简成最简分数。

求一组正整数的最大公因数的方法一般有以下几种：

①列举法。对于求几个较小正整数的最大公因数，可以采用先分别列举出每个正整数的所有因数，再从它们的公因数中找出最大公因数的方法。

②短除法。在可整除所有正整数的条件下，把从小到大的质数依次做除数去除（有时同一个质数可除若干次），直到被除数两两互质时为止，这时将所有除数相乘的积就是最大公因数。

③分解质因数法。根据上面最大公因数的现代数学概念的性质4，可以分别写出被求各正整数的标准分解式，将各分解式中公有的质因数写出。每一质因数都取它在各分解式中的最低次幂，把这些质因数的幂相乘，即得最大公因数。例如24=2x2x2x3，36=2x2x3x3，将这两个数分解质因数后，并将它们公有的质因数的最低次幂相乘---2x2X3=12，所以( 24，36)= 12。

④辗转相除法。在数学中，辗转相除法又称欧几里得算法，是求最大公因数的一种算法。辗转相除法首次出现于公元前300年欧几里得的《几何原本》中，而在我同则可以追溯至东汉出现的《九章算术》。两个正整数的最大公因数是能够同时整除它们的最大的正整数。辗转相除法基于以下原理：两个正整数的最大公因数等于其中较小的数和两数的差的最大公因数。例如252和105的最大公因数是21（252=21×12，105=21×5），因为252-105=147，所以147和105的最大公因数也是21。在这个过程中，较大的数缩小了，所以继续进行同样的计算可以不断缩小这两个数直至其中一个变成零。这时，所剩下的还没有变成零的数就是两数的最大公因数。

四．教学建议

(1)在具体的的生活情境中，理解最大公因数的现实意义

教学中，因为“公因数”和“最大公因数”两个概念联系紧密， 一般同时进行教学。因此，最大公因数的教学同样需要结合具体生活情境，帮助学生理解其现实意义。

例如陈加仓老师在教学时，创设了剪彩带的生活情境：有两根彩带，一根长30厘米，一根长45厘米，如果把它们剪成长度一样的彩带且没有剩余，每根彩带最长是多少厘米？学生通过画图和分别找因数等不同的方法，得出可以剪成1厘米、3厘米、5厘米或15厘米的小彩带，并且没有剩余。1、3、5、15正是30和45这两个数的公因数。其中15是它们的最大公因数。因此，每根彩带最长可剪成15厘米。就这样，学生在解决问题的过程中，由实际生活抽象出了数学概念，并深刻地理解了最大公因数的现实意义。

(2)分类研究求两个数最大公因数的方法，培养学生思维的灵活性

在小学数学中，只要求学生会求两个数的最大公因数。教学时，教师既要关注求两个数最大公因数的一般情况，还要关注其特殊情况，引导学生分类进行研究。对于求两个数最大公因数的一般情况，可以采用多种求法：可以先分别找出两个数的所有因数，再找出两个数的公因数，从而找出最大公因数；还可以采用短除法或分解质因数法等方法。对于求两个数的最大公因数的特殊情况，一般分为两类研究：有倍数关系的两个数和有互质关系的两个数。主要是引导学生在大量实例中找到求它们最大公因数的特殊规律。有倍数关系的两个数，较小数是这两个数的最大公因数。例如4和8两个数具有倍数关系，它们的最大公因数就是其较小数4。有互质关系的两个数，最大公因数是1。例如9和10两个数互质，它们的最大公因数就是1。不同情况的两个数，采用不同的方法去求它们的最大公因数，学生在分析思考的过程中，培养了思维的灵活性。

四．推荐阅读

《小学数学的基础理论》(钟善基、李家骏，北京师范大学出版社，1996)

该书的第二章第二节主要对最大公因数的相关定理进行了详细的论述，第三节对秋最大公因数的方法进行了具体的介绍。