一年级上册︱为什么在教学中要引导学生充分地进行操作，如画和圈？（一年级上册教材第 5 页第 1 题），学生直接就可以数出结果，为什么还要先画圈？

教材中安排的画圈作用主要有两个方面：一是让学生体会物体的数量与圈的一一对应关系，进而促进学生对数的基数意义的理解。二是从实物到圈，再到写出数字，也是帮助学生再次经历数的抽象过程。也就是说，通过上述习题的练习，让学生体会到每一个圈（有时可用其他图形符号，如小三角形、小正方形）可以代表单一物体，这样画圈的过程，就是让学生经历从实物到图形的半抽象过程。而在此基础上，再安排写数，则是从半抽象图形到数符号的进一步抽象过程，即无论是小圆圈，还是小三角形、正方形的数量，都可以用简单的数的符号表示。经过这些逐步递进的活动，将对学生认识数的意义会有较大的帮助，还会促进画图能力的形成以及学生思维灵活性的发展。

二年级上册︱用乘法解决问题，列算式时是否要区分两个乘数的顺序?

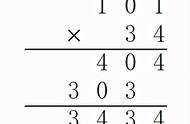
根据《标准（2011 年版）》，相乘的两个数都叫乘数，本套教材中没有刻意区分原来所说的乘数和被乘数。算式“4×6”，既可以表示 6 个 4 相加，又可以表示 4 个 6 相加，即在不涉及具体问题情境的情况下，可以代表两个意义：4×6＝6 6 6 6 或 4×6=4 4 4 4 4 4 都是对的。反之，6 个 4（或 4 个 6）相加既可以用 4×6 表示，也可以用 6×4 表示。也就是一种意义可以用两种方式表示。但在具体的情境中，不同的算式有时表示不同的含义，比如，“有 6 个小朋友，每人有 4 支铅笔，一共有多少支铅笔？”4×6 只代表 6 个 4 相加，当然这个实际问题也可以列出算式“6×4”。

在解决实际问题教学过程时，教师要注意让学生理解各个数的意义，鼓励他们用自己的语言表达算式的具体含义，但列成算式后不必强调两个数的书写位置。同样，在分数乘法的内容中，教材也不区分乘数的位置，处理的方法和整数是一样的，也就是说分数乘整数不但可以表示几个相同分数的和，还可以表示一个数的几分之几是多少。

教材进行这样的处理在数学中是没有问题的，主要是为了减少学生在学习中的“人为”障碍。学生在学习乘法时最重要的是体会乘法的意义。

上海市浦东新区教育学院曹培英老师在“关于乘法运算意义与乘法交换律的教学处理”文章的最后谈到的一段文字非常有道理，特摘录部分内容与大家分享：

事实上，面对用情境图或文字表达的实际问题，如：