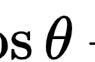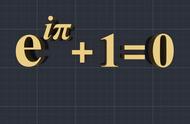作者 | 民间数学家

来源 | 职业数学家在民间

一、上帝创造的数学公式

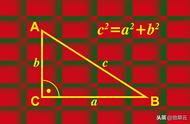
1743年，著名的数学家欧拉在一篇正式发表的论文中首次得到了如下这个结果

(欧拉公式) e^it＝cost isint

其中e是自然常数，其值约为2.718；cos和sin分别是余弦和正弦函数；i是虚数，满足 i²=-1。当t=π时cosπ＝-1，sinπ＝0，于是上面公式变成

(欧拉公式) e^iπ 1=0

第二个公式更广为流传，短短的公式中聚集了五个最著名的数学常数：

0，1，i(虚数)，π(圆周率)，e(自然对数)

因此，第二个公式也被数学家们称为“上帝创造的数学公式”

二、解构欧拉公式

我们来看欧拉公式中的五个常识

0，1，i，π，e

和三个函数

e^x，cost，sin t

其中0和1无需多言，i在我们此前的文章《复数——几何直观和代数运算的交响乐》中也彻底讲明白了。圆周率π就是单位圆(半径为1的圆)周长的一半。还有函数 cost，sin t ，它们分别表示(以原点为圆心的)单位圆周上，逆时针偏离(1,0)点弧长距离为t的点的横坐标和纵坐标，

到了自然函数e和指数函数e^x问题就来了，

自然常数e为什么会称为自然？

指数函数e^x当x为有理数时，可以用乘方和开根号来定义，

对于一般实数是不是要用极限定义？

欧拉公式中指数函数e^x甚至取x值为虚数，那又该如何定义？

这些问题正是欧拉公式给许多人留下神秘印象的原因。要解释清楚欧拉公式和这么多问题，我们该选择从哪里入手作为起点呢？

三，起点

我们选择的起点就是用幂级数定义的函数E(x)

很多人在这里可能要问：

为什么选择这个幂级数作为起点？

因为唯有如此，才能最便捷最有效地理解欧拉公式，请拭目以待！

注意这个函数E(x)对于所有的复数x都是可以定义的，这一点非常重要。

好了，接下来，我们将从这个起点出发，推导出两个方程(微分方程，函数方程)和一个共轭等式，这三者对我们理解欧拉公式都是至关重要的！

(函数方程) E(x)E(y)=E(x y)

我们直接推导这个函数方程：

大家注意推导中最后一步使用了二项式定理，实际上函数方程是二项式定理的生成函数表达式，换句话说

函数方程和二项式定理是等价的。

(除了二项式定理外，还有很多组合恒等式可以写成生成函数的形式，有兴趣的朋友可以自主探索一下。)

好了言归正传，如果我们令