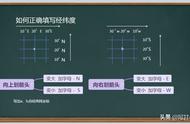
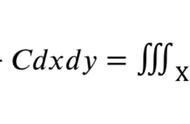学习物理和化学的过程中,会遇到各种各样的图像分析问题。原因是教材和老师授课的过程中,不同学科的内容孤立。数学概念在物理、化学中的用法;数学老师不会讲,物理、化学老师没有讲。结果学生在分析物理化学图像的时候,往往是凭着感觉去做,每次遇到一种新的图像,又要浪费时间和精力,重新去找感觉。在这篇文章里,我会从数学中点坐标的来历,点坐标与函数图像的关系,点坐标在物理化学图像分析问题中的使用方法,跨学科概念如何应用四个方面探索这个问题。
点坐标的由来张三在教室的第三行、第四列,通过这句话我们能意会到,说的是张三在教室中的座位。把这句话改成“张三的座位在教室的(3,4),”。坐标中,逗号前面是行,后面是列。懂得这个数学潜规则的人就知道,说的是第三行、第四列;不懂的人,意会过来,就有说成第四列,第三行的。潜规则就是概念,点坐标(3,4)就是一个表达位置的概念。

哪个座位是(3,4)?
插两句话,辅导过小学生的都会碰到这样头铁的小朋友,同学之间的潜规则他们比谁都懂,数学的潜规则绝不接受。把掌握数学概念学习的意义等同于掌握潜规则的意义,跟他们多讲讲,概念学习就开窍了。
又一个问题来了,光知道(3,4)的概念,生活中还是没有用。军训队列练习,一个向左转,哪个是行,哪个是列?一个向后转,第三行是从前往后数,还是从后往前数?第四列是从左往右数,还是从右往左数?全乱了套了,弄不清楚了。讲不清楚怎么办?难不倒数学,弄一个叫原点的概念出来就是了,制定个潜规则,原点上下为列,原点左右为行。把队列里张三的位置标记成(0,0),这样不管左右转,前后转,队列里面每个人的位置不就清楚了吗。
老是打补丁,看起来一点也不数学啊!于是,找一张纸,先画两条互相垂直的直线,横向直线右边画个箭头叫x轴,代替原来的左右;纵向直线上边画个箭头叫y轴,代替原来的前后;直线交点就叫原点,从原点出发,把直线等分成一格一格的线段。你看,平面直角坐标系的概念又来了,要掌握的潜规则真多!
点坐标与函数、函数图像的关系函数是啥?张三去菜市场买菜,挑了2斤鸡蛋,24元;1斤猪肉,24元。老板算账的时候说:1斤24元,2斤24元,一共48元。张三买的东西重量不一样,买一样东西花多少钱有定数,这时候就说张三买一样东西花的钱是重量的函数。你看,又弄出一个潜规则,不能倒过来这样说,张三24元买了一斤猪肉,因为24元还能买2斤鸡蛋。
一斤鸡蛋两元,买了斤,花了元,那么了和之间的关系就是。买1斤,;买2斤,;买3斤,...。数学家一看,这样写啥时候写到头啊!而且看起来一点也不数学。得了,再弄一个潜规则吧,规定数对(,)中逗号前表示的值,逗号后表示的值。这样上面一段可以写成,,...。写完再一看,这不就是点的坐标吗?干脆把这些点给它画到直角坐标系里面去,省得还得写这一长串数字。嗯,函数、图像,这个方法就叫数形结合吧。
数形结合,平面直角坐标系里面的点坐标,横坐标表示自变量,纵坐标表示函数。
点坐标在物理化学中的应用物理、化学中也有直角坐标图像,比如速度-时间图像,密度-体积图像,溶解度-温度图像等。这些图像本质上也是函数图像,和函数图像一样,曲线上每个点的坐标都表示对应函数的一个解。但和数学中的函数图像又不一样,物理化学的函数图像上的点坐标有单位,能和具体的场景对应。如下图

读图的时候,要标记点的坐标为,必须带单位。还要明确A点对应的场景-当滑片P位于b端时。B点的坐标为,B点对应的场景-当滑片P位于a端时。同时要找到图像对应的函数关系式-。这样,图像表达的内容你才是完全掌握了。
最后,物理化学中研究图像时,必须明确点坐标的意义,对应的场景,函数关系式这三项内容