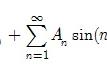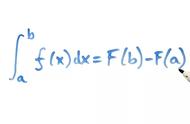作者 | 张海潮（台湾大学数学系退休教授）

来源 | 数学传播，45卷2期，pp.12-17，好玩的数学获授权转载，在此感谢！

如图一所示, 微分是求函数 图形上一点切线的斜率。

而当 时, 积分则是求 函数图形下方, 轴上方之间的面积, 如图二所示, 阴影部分代表介于, , 轴和函数图形之间的面积(注一)。在图一的情形, 求一条直线的斜率, 需要知道两点, 因此作法是在图形上除了点 之外, 另在附近取一点, 如图三所示(注二)。

先求 线的斜率

然后再令 趋近于, 将所得的极限定为切线的斜率。式(1) 一方面是图三中割线 的斜率, 另一方面式(1)也代表当 变动到 时, 的平均变率(average rate of change), 而当 时, 式(1)的极限便是 在 点的瞬间变率 (Instantaneous rate of change at )。

平均或是瞬间变率的考量可以针对任意的函数, 一旦能够掌握 在 的极限 便可以从 反求, 这正是牛顿当年发现微积分基本定理的切入点。牛顿首先将图二改成图四(注三)。