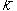导数,在高考中,常以压轴题出现。下面时间我们一起研究高考数学总复习专栏第794课:与导数相关的新定义问题压轴题,条件给出了最大值函数的概念。涉及的函数类型有指数函数、对数函数、三角函数和一、二次函数,函数类型考查得非常的全面。

第一问:证明,当X大于等于1的时候。F(x)大于等于零。当X小于1的时候,F(x)小于零。

因为F(x)是超越函数,我们需要通过求导数,通过导数的符号研究函数的单调性和最值,进而确定函数的符号。
通过求导并分解,为了判断符号,可以采用我们前面强调的核心方法——类穿根法,来判断导数的符号。通过解方程发现,本题在使用穿根法时用到类二重根问题。

由于导数恒大于等于0,判断出原函数为增函数,通过判断临界点的函数值进而确定原函数的符号。
第二问:判断是否存在参数a,使得最大值函数大于等于零永远成立。其实第一问已经给我们解决思路了。第一问,当X大于等于1的时候,这个函数已经大于等于零了。

根据最大值函数的定义和对数函数的定义域,我们只需要研究-1<x<1时g(x)≥0恒成立就行了。
G(x)是一个难点,其导函数的符号难以判断,我们只能借助其二阶导数、隐零点问题、三角函数有界性及找点卡根来判断一阶导数的符号,进而确定函数的符号。
原函数、导数和二阶导数三个符号图是解题关键。
在找点卡根问题中,借助我们独创的内置常数法进行秒*。
当然了,本题可以通过第二个方法进行1分钟速解,借助数形结合,先猜后证,从而确定参数的值。

很多朋友问,到高三了,怎样复习呢?实际上,大家都上过学,都明白,刷题是没有用的,题海战术徒劳而无功,需要从考点出发,系统梳理,形成知识系统是关键,以不变应万变。如需系统学习请选用高考数学总复习20天一栏通关专栏,包括考点总结、题型分类、方法技巧、课后训练、高考预测,并为已使用的朋友准备了6000页的大资源库方便大家针对性选用。请看下面的目录和小卡片,需要这个专栏的请联系。

★新高一的朋友请使用下面专栏:
更多内容: