动点最值问题是初中数学的难点了，将军饮马、阿氏圆、胡不归、费马点、隐圆模型、瓜豆原理等，考点挺多，需要同学们总结不同模型的特征，题目给出一些条件符合哪个模型，我们就可以快速解题。

最近在网上看到某附中的中考模拟题，答案给的思路不太典型，一般同学们不太容易想到，这里介绍另一种思路。

数学题本质就是解读条件或者结论，跟所学相联系，去求解。

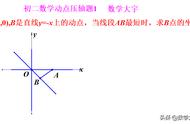
例题：如图，△ABC中，BC=4，∠BAC=45°，则√2AB AC的最大值为_____

（视频讲解在文末）

分析：这个题目初看条件非常简单，毫无头绪，结论这里非常典型，√2AB AC最大值，这个结论形式类似阿氏圆、胡不归的最值类型，那就可以类比同样的方法把√2AB去转化到某条线段，再与AC结合求最值。

①√2AB怎么转化呢？√2一般是等腰直角三角形中出现的比例关系，所以构造以AB为直角边的等腰直角三角形；

②如上图，AB绕点A顺时针旋转90度，得到等腰直角三角形ABD，BD=√2AB；

③BD=√2AB，但是BD与AC不相连，不符合阿氏圆、胡不归的三点共线最值类型，那得想个办法让BD和AC连起来;

④如上图，把BD从点B平移到点A，得到平行四边形ABDE，AE=BD=√2AB;

这个题目巧的是，E、A、C三点始终共线，∠EAD=45°，∠DAB=90°，∠BAC=45°，这三个角加起来刚好是平角180°；

分析到这里，这道题目中要求的√2AB AC最大值就转化到求EC的最大值，点C是定点，找出点E的轨迹，就可以得到EC最大值；

接下来，熟悉主从联动模型的同学就笑了，点E的轨迹不就是个圆嘛，因为点A这里定角定长，A的轨迹是圆，那么点E轨迹也是圆。

但是需要简单证明一下，如果∠BEC是定角，那么点E轨迹是圆。

连接EB，交AD与点F，因为∠BEA不好直接求度数，可以迂回一下；

∠DEA=45°，如果∠DEF度数是定值，那么∠BEA度数也是定值了；

DF=DA/2=DE/2；

tan∠DEF=1/2；

∠DEF度数是定值，所以∠BEA度数也是定值；点E轨迹是圆；

当EC是直径是，EC长度最大！

此时∠EBC=90°

直接求EC长度，初中常考两种方法，一是勾股定理，二是相似三角形；勾股定理只有一个BC=4，没办法求，所以考虑相似三角形。

过点F作FG⊥EA于点G，为什么选点F呢，F点周围的线段长度之比容易求出来，而且△EFG∽△ECB

如上如所示，即可求出EC长为4√10

即√2AB AC最大值为4√10

-视频讲解-