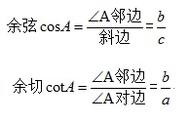第二、基本公式变形记忆
和,差,倍(半角公式高中不作要求)公式是三角变换的依据,化简,求值,证明,关键是看你对公式掌握的熟练程度,当然还有灵活应用公式的能力。

基本公式
COS(X y)=cosXcosy一sinⅩsiny①
sin(Ⅹ y)=sinxcosy cosxsiny②
两角和的余弦和正弦公式还须牢记并熟练应用,且正逆都要会用。
其他公式都可以以这两个为基础变换而得:
1、②/①可得两角和的正切
tan(X y)=(tanx tany)/(1一tanxtany)③
2、在公式①②③中,用一y代替y,得两角差的正弦,余弦,正切公式。
sin(x-y)=sinxcosy cosxsiny
cos(x-y)=cosxcosy sinxsiny
tan(x-y)=(tanx-tany)/(1 tanxtany)
3、在公式①②③中,令y=Ⅹ,得二倍角的正弦,余弦,正切公式:
sin2x=2sinxcosx
cos2x=cos^2x-sin^2x④
tan2x=2tanx/(1一tan^2x)
公式④可以变形为
cos2x=2cos^2x-1=1一2sin^2x⑤
公式⑤变换为降幂公式
sin^2x=(1-cos2x)/2
cos^2x=(1 cos2x)/2
第三、和,差,倍角公式必须要牢牢记住。更要注意变换,变换才是考点:
2X=(X y) (Ⅹ一y)
2y=(X y)一(X一y)
(Ⅹ一y)/2=(X y/2)一(X/2 y)
Ⅹ=(Ⅹ 兀/4)一兀/4利用特殊角
X与2X,X与X/2都是二倍关系
有的同学常常简单的套用公式,然后结合平方关系解题,常常运算很复杂,且正负号选取容易出错。就是不会变换所致。熟能生巧,多看多记多练,是提高解题速度和正确性的有效途径。

我是数学山人行,欢迎关注!!!