加密和解密使用的是两个不同的秘钥,这种算法叫做非对称加密。非对称加密又称为公钥加密,RSA只是公钥加密的一种。
数字签名 && 数字证书
现实生活中有签名,互联网中也存在签名。签名的作用有两个,一个是身份验证,一个是数据完整性验证。数字签名通过摘要算法来确保接收到的数据没有被篡改,再通过签名者的私钥加密,只能使用对应的公钥解密,以此来保证身份的一致性。
数字证书是将个人信息和数字签名放到一起,经由CA机构的私钥加密之后生成。当然,不经过CA机构,由自己完成签名的证书称为自签名证书。CA机构作为互联网密码体系中的基础机构,拥有相当高级的安全防范能力,所有的证书体系中的基本条件就是CA机构的私钥不被窃取。
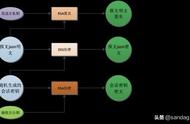
CA证书的生成过程如下:

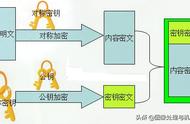
证书参与信息传递完成加密和解密的过程如下:

欧拉函数
互质关系:互质是公约数只有1的两个整数,1和1互质,13和13就不互质了。 欧拉函数:表示任意给定正整数 n,在小于等于n的正整数之中,有多少个与 n 构成互质关系,其表达式为:

其中,若P为质数,则其表达式可以简写为:
情况一:φ(1)=1;
1和任何数都互质,所以φ(1)=1;
情况二:n 是质数, φ(n)=n-1;
因为 n 是质数,所以和小于自己的所有数都是互质关系,所以φ(n)=n-1;
情况三:如果 n 是质数的某一个次方,即 n = p^k ( p 为质数,k 为大于等于1的整数),则φ(n)=(p-1)p^(k-1);
因为 p 为质数,所以除了 p 的倍数之外,小于 n 的所有数都是 n 的质数;
情况四:如果 n 可以分解成两个互质的整数之积,n = p1 × p2,则φ(n) = φ(p1p2) = φ(p1)φ(p2);
比如,φ(30)=φ(5×6)=φ(5)×φ(6)=4×2=8。此种情况可以通过"中国剩余定理"证明,证明过程不再本文讨论范围内。
情况五:基于情况四,如果 p1 和 p2 都是质数,且 n=p1 × p2,则φ(n) = φ(p1p2) = φ(p1)φ(p2)=(p1-1)(p2-1)
例如,φ(39) = φ(3×13) = φ(3)φ(13)=2 × 12 = 14;
而 RSA 算法的基本原理就是欧拉函数中的第五种情况,即: φ(n)=(p1-1)(p2-1);
模反元素
如果两个正整数 a 和 n 互质,那么一定可以找到整数 b,使得 ab-1 被 n 整除,或者说ab被n除的余数是1。这时,b就叫做a的“模反元素”。欧拉定理可以用来证明模反元素必然存在。

可以看到,a的 φ(n)-1 次方,就是a对模数n的模反元素。
RSA算法原理
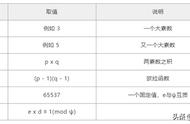
1、随机选择两个质数并计算乘积
n=p x q = 3233,3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。
在实际使用中,一般场景下选择1024位长度的数字,更高安全要求的场景下,选择2048位的数字,这里作为演示,选取p=61和q=53;
2、计算n的欧拉函数φ(n)。
因为n、p、q都为质数,所以φ(n) = (p-1)(q-1)=60×52= 3120
3、随机选择一个整数e,条件是1< e < φ(n),且e与φ(n) 互质。
1< e <3120,注意,这里是和φ(n) 互互质而不是n!假设选择的值是17,即 e=17;
4、计算e对于φ(n)的模反元素 d
模反元素就是指有一个整数 d,可以使得 ed 被 φ(n) 除的余数为1。表示为:(ed-1)=φ(n) y --> 17d=3120y 1,算出一组解为(2753,15),即 d=2753,y=-15,也就是(17 2753-1)/3120=15。
注意,这里不能选择 3119,否则公私钥相同.
5、生成结果
公钥:(n,e)=(3233,2753) 私钥:(n,d)=(3233,17)
为什么无法破解
公钥是公开的,也就是说 m=p*q=3233 是公开的,那么怎么求 e ?e 是通过模反函数求得,17d=3120y 1,e是公开的等于 17,这时候想要求d就要知道 3120,也就是 φ(n),也就是 φ(3233),说白了,3233 是公开的,你能对 3233 进行因数分解,你就能知道 d,也就能破解私钥。
正常情况下,3233 我们可以因数分解为 61*53,但是对于很大的数字,人类只能通过枚举的方法来因数分解,所以RSA安全性的本质就是:对极大整数做因数分解的难度决定了 RSA 算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。
人类已经分解的最大整数是:

这个人类已经分解的最大整数为 232 个十进制位,768 个二进制位,比它更大的因数分解,还没有被报道过,因此目前被破解的最长RSA密钥就是 768 位。所以实际使用中的 1024 位秘钥基本安全,2048 位秘钥绝对安全。