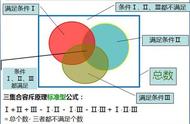
见左图。左边的圆是集合A，右边的圆是集合B。两个圆相交叠的红色部分既属于A也属于B，两个圆外面的白色部分既不属于A也不属于B，是集合D。元素总数=A的元素数 B的元素数-A∩B的元素数 D的元素数。为什么要减去交集呢？因为在计入元素总数时，这部分被重复计入了。这是二元容斥原理。二元问题，是先把这两个集合全包容进来，再把重叠部分排斥出去。有容有斥，这就是容斥原理。

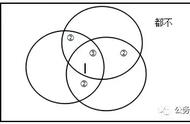
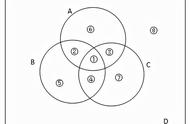
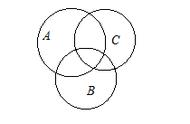
三元容斥就麻烦啰。见右图，粉色是A与B共有的部分，黄色是B与C共有的部分，橙色是C与A共有的部分。这三块，都是被多计入了一次。黑色是A、B、C三个集合共有的部分。D是A、B、C以外的部分。元素总数=A的元素数 B的元素数 C的元素数-A∩B的元素数-B∩C的元素数-C∩A的元素数 A∩B∩C的元素数 D的元素数。计算元素总数时，粉色区域、黄色区域、橙色区域都被重复计算了两次，需要减去，这个与二元容斥相同。黑色区域先在“ A的元素数 B的元素数 C的元素数”时被重复计入了三次，后又在“-A∩B的元素数-B∩C的元素数-C∩A的元素数”被扣去了三次，它等于被无视了，因此我们在最后得把它加上去。这个公式很长很复杂不好记忆，改成一句简单的话：三集合相加，减去三个二元交集，加上三元交集。三元容斥是先把三个集合全部包容进来，后排斥掉三个集合的两两重叠部分，这样，把三集合的交集也排斥出去了，最后再把这个包容进来。因此，三元容斥是容、斥、容。

容斥原理不仅可用于集合问题，其它数学问题包括几何问题，都有可能用到。