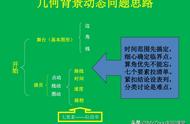
在图形的运动转变环节中,必须认真研究图形的变化规律性,把握积极自变量与从动变量,情景交融,从这当中探索出两者相互关系,利用函数关系处理。
数学课关键在于训练,在实战中要注重总结解题技巧和方式。
有时候我们做了多张试卷都是在训练一种解题构思和方法,这时候必须举一反三,一题多解。
多解归一是学数学最有效的方法,在探索中和体验中找到解题的切入点,不会深陷题海战术不能自拔,还给自己带来了压力和压力。
答题思路
在数学考试中,很多同学往往因为时间不够造成数学试题不能写完,考卷评分不太高。
把握解题思想可以帮助同学们快速找到解题构思,节省考虑时长。
函数与方程思想
函数公式思想就是指应用健身运动转变的观点,分析和科学研究数学里的排列与组合,通过建立函数关系应用函数的图像和特性去思考问题、转换问题和解决困难。
方程式思想,是以问题的排列与组合下手,应用数学语言将问题转化为方程式或基本不等式实体模型去解决问题。
同学们在解题时,可利用转换思想开展函数与方程之间互相转化。
独特与一般的思想
用这种思想解单选题有时候尤其合理,因为一个出题在普遍意义上创立时,则在特殊情况下也必然创立,依据这一点,同学们能直接明确单选题里的正确选项。
值得一提的是,用这种思想方法去探索论述题的推导对策,也同样有效。
极限值思想
极限思想解决问题一般过程为:
1、针对所愿的未知量,先想方设法设计构思一个与它有关的自变量;
2、确定这自变量根据无尽全过程的结果就是所愿的未知量;
3、对象(等差数列)并利用极限值计算法,得到结论或利用图形的极限值部位立即数值。
分类讨论思想
同学们在解题时常常会遇到这样一种情况,解到某一步后,不能再以统一的方式、统一的算式继续进行下来。
主要是因为被科学研究的对象包含了多种多样状况,这就需要对各种情况进行归类,并逐类求得,之后综合性梳理得解,这便是分类讨论。
造成分类讨论的原因很多,数学定义本身具有多种多样情况,数学课运算法则、一些定律、公式的限定,图型部位的不确定性,转变等均可能引起分类讨论。
提议同学们在分类讨论解题时,要做到标准统一,不重不漏。
「傻刷题」比不上「巧做题」,把握数学课解题思想是解释算术题时不可或缺的一步。

提议同学们正在做题目类型练习之前先掌握数学课解题思想,把握解题方法,并把做过的题型进行区划,便于在考试中得心应手。