三角形中位线性质定理的应用是中考的热门考点之一，该定理常用来证明线段相等或计算线段的长度。学习该定理应掌握以下三个方面内容。

一、理解并掌握三角形中位线的性质定理。

1、三角形的中位线:连接三角形两边中点的线段叫三角形的中位线。

2、三角形中位线性质定理:三角形的中位线平行于三角形的第三边且等于第三边的一半。

3、命题证明:

1、分析命题:

题设:如果一条线段是三角形的中位线。

结论:那么这条线段平行于三角形的第三边且等于第三边的一半。

2、画出图形:

分析与图形有关词语是:①三角形②中位线

3、写出已知和求证

已知:△ABC中，点D、E分别是AB，AC的中点

求证:DE//BC，DE=1/2BC

4:证明:

分析:证明某线段等于另一线段的一半时，常常延长较短线段的一倍，再证明线段相等。证明线段相等常用方法是三角形全等，本次利用平行四边形对边相等证明线段相等。

证明:延长DE到F，使DE=EF，连结CF。

∵AE=EC，DE=EF

∴四边形ADCF是平行四边形

∴AD//CF且AD=CF

∴BD//CF且BD=CF

∴四边形BCFD为平行四边形

∴DF=BC且DF//BC

∵DE=1/2DF

∴DE//BC且DE=1/2BC。

例1、已知在△ABC中，D，E分别是AB，AC的中点，F，G分别是AD，AE的中点，且FG=2cm，则BC长是多少？

解∵F，G为AD，AE中点

∴DE=2FG=2×2=4cm

同理BC=2DE=2×4=8cm。

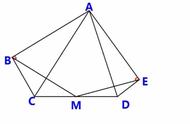
例2、如图，D是△ABC内一点，BD丄CD，AD=7，BD=4，CD=3，E，F，G，H分别是AB，

BD，CD，AC的中点，则四边形EFGH的周长为( )A，12 B，14 C，24 D，21

解:∵BD丄CD

∴∠BDC=90°

在Rt△ADC中，BD=4，CD=3

由勾股定理可得BC=√BD² CD²=√4² 3²=5

∵E，F分别是AB，BD的中点，

∴EF=1/2AD=1/2×7=3.5

同理HG=1/2AD=3.5

EH=FG=1/2BC=1/2×5=2.5

∴四边形EFGH周长=2×(3.5 2.5)=12

二、应用三角形中位线性质解决四边形的有关问题

例1、顺次连接四边形各边中点所成的四边形一定是平行四边形。