前面之前的数据结构知识,介绍了矩阵的三元组表示法,当然之前只介绍矩阵运算中的转置,至于乘法运算以及加减运算,之前没有介绍,但是三元组表示法缺陷不小,比如当矩阵运算的非零元素个数和位置在操作工程中变化较大时,如果还是用三元组表表示法来计算,并且还要保持三元组表以行序为主的方式存储,那么可能要大量移动数据元素,这时三元组表表示法实用性就欠缺了,今天暂时只介绍一下稀疏矩阵的十字链表存储方式,当然不稀疏也行,该方式的灵活性就大大增强了,它能灵活插入新产生的非零数据元素,并且也能灵活删除因运算变为0的新元素,所以说掌握矩阵十字链表存储方式,还是很不错的。下下篇在介绍广义表之前,会举一个用十字链表进行矩阵的乘法或加法运算。

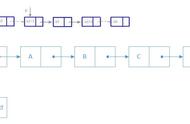
既然是链表,那么肯定得有结点,结点肯定以结构体方式定义,那么该结构体应该有哪些成员呢?描述一个矩阵中的非零元素,那么肯定需要位置信息,数据元素大小,因此就相当于前面三元组表表示法,那么包含该非零数据元素的行、列、以及该非零数据元素的大小,以及两个指针成员,一个用于连接同一行的非零数据元素,一个用于连接同一列非零数据元素。先看一下示意图吧:

十字链表示意图
我们可以声明该结构体类型如下:

十字链表结点声明
上面就是结点结构体的定义。
我们下面就需要定义一个矩阵的具体信息结构体,上面示意图可以看出,矩阵中每一行每一列都需要一个头指针,根据每个头指针可以扫描遍历每个非零数据元素,因此对于有m行的矩阵,我们需要定义m个行头指针,对于n列的矩阵,我们需要n个列头指针,而且还需要矩阵大小的信息,包括行数列数,以及非零数据元素个数,因此得到下面结构体,如下: