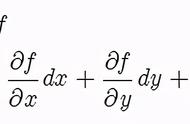大年初六，新年已经逐渐走向尾声，有没有小伙伴正在忙于补写作业呢？

不论在什么时候，记公式总是一件令人头秃的事情，枯燥又乏味。有没有什么办法能够更简单快捷地记住各种公式呢？去网络上查找一下，常见的答案要么是不需要记，理解了，会推导就行，要么是好记性不如烂笔头，多写多用自然就记住了。

那么记公式真的没有任何捷径可言吗？当然有了，这里小编精心整理了几点小技巧供大家参考。

妙用公式

在不是纯数字的情况下，公式中等号两边需要拥有相同的单位。就如同现实中一磅不能与一镑划等号。

与此同时，公式中的很多符号或常量也拥有自己的单位，通过单位就能够知晓某些量的含义，例如密度的单位常为，其公式便为质量/体积。

这里可以参考一个经典的单摆实例。

单摆

上图展示的是一个理想的单摆，小球质量为,绳长为,单摆所在位置的重力加速度为,单摆初始方位角为,现想要求出单摆的周期是多少。通常的推导思路是进行受力分析，列出牛顿方程或者写出拉式量，得到微分方程，求解获得的表达式。在小角度的情况下，单摆周期有一个简单的表达形式，但是这个公式使用的频率并不高，即使有背过也很容易记不清楚，只能重新推导一遍了吗？

通过对单位的分析，或许可以更加简单。假设

整个过程中一共涉及了5个物理量，、、、以及。在国际单位制下单位分别为、、、和。为两个长度之比，可以由的单位导出，的单位可以用与的单位的组合来表示。如果把、与取作基本单位系统

上式中取了、、的值为新单位系统下的单位1，等号右端只与有关，可以简写为从而得到

这样我们可以简单的得出结果，与成正比，与成反比，与无关，而的具体形式则需要通过理论或实验求得。

如果初始方位角是个小量，上式可以进一步化简，首先从单摆的对称性可以断言是一个偶函数，对其在处进行泰勒展开有