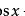上方超级数学建模可加关注
传播数学干货,学会理性的方式去思考问题
《数学欣赏》:历久弥新的通俗数学经典
使我感到异常震惊的是,所有那些写得最好而且最重要的阐述数学方法的书,在这里 [法国]却几无学生知晓(在我看来,甚至可能没被译为法文)。这些书有拉德梅彻–托普利茨写的《数学欣赏》、希尔伯特和康福森写的《直观几何》、 柯朗和罗宾斯写的《数学是什么》、波利亚写的《怎样解题》 和《数学与猜想》、克莱因写的《数学在19世纪的发展史》。
沃尔夫数学奖得主、数学教育家阿诺德(V. I. Arnold)
12岁时,我开始对数学感兴趣。我从我的叔叔 Albert Kornfeld 那里学到很多,他 是一位优秀的数学家。当他还是高中生时,曾在重要的竞赛中获奖;后来他成为工程师。之后, 有一位专业的老师辅导我,她是一位很好的女数学家,名字叫 Rózsa Péter。她是逻 辑学家,写过关于递归函数的第一本书。她也是一位杰出的老师。我们所读的第一本书是 Rademacher–Toeplitz 的书,英文书名是《数学欣赏》(The Enjoyment ofMathematics)。书中每个篇目都很短,只有五六页,对刚开始学习数学的学生很合适。即便时至今日,我仍会推 荐这本书给对数学有兴趣的年轻人。
沃尔夫数学奖得主、Abel 奖得主拉克斯(PeterLax)
我第一次在课外邂逅数学是9岁时, 我的母亲给我买了 Rademacher 和 Toeplitz 的一本书《论数与形》,它对我产生了极大的影响。 尽管大部分内容我都读不懂,但我一直都很兴奋。 那种似懂非懂、无法理解却使我好奇、欲罢不能的神秘感,至今我都记得。
沃尔夫数学奖得主、Abel 奖得主格罗莫夫(MikhailGromov)
笔者在大学期间读过的所有数学书中,拉德梅彻(Hans Rademacher)与托普利兹(Otto Topelitz)合著的《数学欣赏》是最让我激动的一本。今天我想把它推荐给所有对数学感兴趣的中学生和大学生(甚至有人建议,部分内容可以让小学生尝试)。
《数学欣赏》原书是德文的,标题为《论数与形》(VonZahlen und Figuren)。中译本书名“数学欣赏”,译自同名英译本TheEnjoyment of Math(普林斯顿大学出版社,1957年)。
如本文开篇的引语所表明的,在许多大数学家年少时,这本书曾启发了他们对数学的兴趣。除了阿诺德、拉克斯和格罗莫夫,还应该提到德国数学家、沃尔夫数学家得主希哲布鲁赫(Friedrich Hirzebruch, 1927‐2012)。
在为《成为科学家的100个理由》的撰稿中,希哲布鲁赫提到这本书也是他的数学启蒙书:
我喜欢拉德梅彻和托普利兹的《论数与形》,该书出版于1933年, 我大约是在1938年前后开始阅读,当时并不知道两位作者已经由于受纳粹迫害而离开了德国。 1940年,托普利兹在耶路散冷逝世。 1957年朱克曼(Herbert S. Zuckerman)将此书译成英文《数学欣赏》出版,并由当时已经移居费城的拉德梅彻撰写了一篇题为“热爱数学”的前言。 我至今还记得该书1933年版导言中的一段话:“……本书不想重复其他学科能够为读者展示的那些事实, 而是要强调现象的类型,以及提出问题和解决问题的方法。”他们的作品表明,如同音乐之美,数学之美能够让初学者爱好者在力所能及的程度上见仁见智的去欣赏。 按照这种思路与写法,高中生已经能够理解数学原理,并感受其美妙。
好老师对学习数学至关重要。幸运的是,我遇上了如我的父亲和《数学欣赏》这样优秀的引路人。 下面我举一些当时自己认为特别有趣,而且能够被高中生理解的书中例证。 素数数列,涉及到算术数列中无穷多个素数的问题;不可通约线段和无理数问题,当古希腊人意识到正方形的边与对角线之比并非有理数时,他们感到极度的绝望; 垂足三角形的最小性质,可用于解决如下问题,给定一个锐角三角形,求周长最短的内接三角形(就像在一张锐角三角形台面上打弹子球一样)。 其他的例子还有毕达哥拉斯数和费尔小定理,循环小数以及决定其循环节长度的数论问题,等等。 为了类似的有趣问题,我在课余时间更多地接触数学,乐此不疲。我一直认为,学生有机会通过老师了解这些数学瑰宝是很幸运的,非常有助于他们从繁琐的日常解题中解放出来,体会数学的真正趣味。
而菲尔兹奖得主马宁(Yu. I. Manin)曾写过一篇题为“Von Zahlen und Figuren”的文章,并在脚注中注明:“用这一标题是为了纪念 Hans Rademacher 和 Otto Toeplitz, 他们的书多年前曾令我痴迷。”
作者:托普利兹与拉德梅彻
常常出现这样的情况,往往读完一本书尤其是科普书,我们对作者本人的情况仍知之甚少。有鉴于此,特别是考虑到本书的两位作者所取得的非凡成功,我们这里对他们的生平略作介绍。
托普利兹(1881–1940)
Otto Toeplitz,犹太人,1881 年出生于德国布雷斯劳,父亲和祖父都是数学教师。 他在布雷斯劳大学学习数学,1905 年取得代数几何方向的博士学位。1906年前往数学圣地哥廷根,1907 年成为那里的无薪讲师。当时的哥廷根有 Klein, Hilbert,Minkowski 等名教授,与 Toeplitz 一起切磋琢磨的年轻人则有玻恩(Max Born)、库朗(Richard Courant)和海林格(Ernst Hellinger),布雷斯劳是他们学生时代的交集。作为四个人中最年长的,正是 Toeplitz 推动着其他人前往数学的麦加哥廷根。Toeplitz 曾与海林格合作,撰写过论文和专著。玻恩比 Toeplitz 小一岁,是其他三人中受 Toeplitz 影响最深的,他在晚年出版的自传中,回忆起在他的学生时代,Toeplitz 对他的影响:
上课时,我们总是喜欢一起坐在前排,在旁边坐着的一些人中,有些在我日后的 生涯中发挥过一定作用,因此我要在这里提一提。 Otto Toeplitz 就是其中一位,他比我高一年级。 他的父亲是个犹太人中学的校长,同时也是一位数学家。 从儿子一出生起,他唯一的愿望就是把独子培养成数学家,并以此为目标教育孩子,最终取得成功。对我来说,这一切都是新的天地。我之前几乎从未 听说过高斯的名字,更不用说欧拉、拉格朗日、 柯西、黎曼、维尔斯特拉斯和其他人了。但对 奥托来说,他们都是熟人,甚至是密友。他不仅知道这些数学家的主要科学著作的概略, 还知道许多有关他们生活以及人品方面的故事。 他很快就喜欢上我,并开始按照自封的教师指点 初学者那样行事。我必须说,多亏了他,特别是他最早引导我步入数学学科的殿堂。在人类所有知识中, 数学是最古老、最有连续性的一门学科。
在希尔伯特的影响下,Toeplitz 在哥廷根的七年里研究泛函分析,取得了重要成果,例如得到了现在以他命名的 Toeplitz 矩阵、Toeplitz 算子。有鉴于 Toeplitz 相关工作的重要性,我们介绍他 1911 年的一项著名成就。希腊数学家卡拉西尔德瑞(C. Carathéodory)在 1907 年曾考虑下述问题:当复数


可以扩充为单位圆内的解析函数

使得