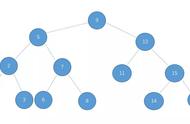
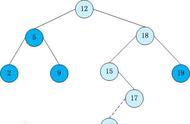
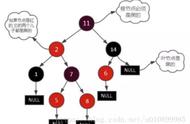
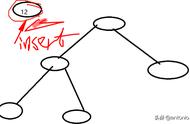
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

2.1. 每个结点不是红色就是黑色
2.2. 根节点是黑色的
2.3. 如果一个节点是红色的,则它的两个孩子结点是黑色的(不会出现连在一起的红色节点)
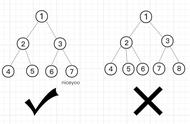
2.4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(在计算一条路径中黑色节点个数的时候要带上叶子节点,因为叶子节点也是黑色的,也就是空节点)。
2.5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)(为了保证空树也是红黑树)
2.6.红黑树确保没有一条路径会比其他路径长出俩倍(红黑树前面的性质保证了当前的性质)

3.1. 带头节点的红黑树
这里我们将红黑树的实现给为带头的红黑树,因为红黑树是map和set的底层数据结构这里我们实现出来红黑树就可以直接用当前我们实现的带头红黑树来实现map和set至于头节点的给出是为了方便于map和set的遍历,在STL中我们区间给出都是左闭右开区间的,既然红黑树作为map和set的底层数据结构那么我们就一定有位置要来放map和set的迭代器,那么就可以将begin位置的迭代器放在head的左,end位置的迭代器可以放在head位置。这里我们将红黑树头节点的颜色给为红色。

3.2. 红黑树的节点