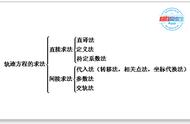
高中数学分为必修和选修，打眼一看，也许觉得选修内容是没多大用的，甚至会认为不会考，那就大错特错了。在选修中曲线方程你是不得不注意的，虽然在选修课本里，但每年高考题是必考内容。曲线有抛物线，双曲线，椭圆和圆。考试中一般是与直线联立出题。因此一定要把这些曲线的方程，特点，及参数牢记，对直线也要特别熟悉。这类题不算难，主要是要联立化简。下面看一道题的解法：

这是一道关于抛物线的题，第一问求定值。既然是定值，那么这个值应该是可以求出来的。所以要设直线方程的斜率k，如果直线与X轴垂直，那么是没有斜率的。所以这问要分两种情况，即斜率是否存在。下面是解法：

看第二问，是找是否存在直线满足条件。这样的问法，一般情况是存在的，看看我的做题思路。

解决这个问题，重点在理解圆中弦的意义及弦长的计算方法，另外，做这类题不能怕麻烦，怕计算，在计算中记得不要出错，否则所有的计算就黄了。下面是这题的解法：

为什么a=1？因为当a=1时，根号下的值与x1无关了。

总得来说，这类题就是这样，千万不要怕麻烦，不要见到这样的题就怕了，自己先放弃就不会得分了。题真的不难，一定要掌握好基础知识，从课本抓起。好了，今天就到这，希望高三的学子每天进步一点点。（作者目前在医院，望谅解用纸不好看）