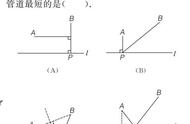
费马点的定义：数学上称，到三角形3个顶点距离之和最小的点为费马点。

它是这样确定的：

1. 如果三角形有一个内角大于或等于120°，这个内角的顶点就是费马点；

2. 如果3个内角均小于120°，则在三角形内部对3边张角均为120°的点，是三角形的费马点。

费马点的性质：费马点有如下主要性质：

1．费马点到三角形三个顶点距离之和最小。

2．费马点连接三顶点所成的三夹角皆为120°。

费马点最小值快速求解：

费尔马问题告诉我们，存在这么一个点到三个定点的距离的和最小，解决问题的方法是运用旋转变换．

秘诀：以△ABC任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值