1、一元二次方程根的情况
△=b2-4ac(前提必须化成一般形式 ax2 bx c=0) 当△>0 时,一元二次方程有 2 个不相等的实数根; 当△=0 时,一元二次方程有 2 个相等的实数根; 当△<0 时,一元二次方程没有实数根
2、平行四边形的性质:
① 两组对边分别平行的四边形叫做平行四边形。
② 平行四边形不相邻的两个顶点连成的线段叫它的对角线。
③ 平行四边形的对边相等并且平行,对角相等,邻角互补。
④ 平行四边形的对角线互相平分。
★菱形:
① 一组邻边相等的平行四边形是菱形
② 菱形的四条边相等,对边平行,两条对角线互相垂直平分,每一组对角线平分一组对角。
③ 判定条件:定义、对角线互相垂直的平行四边形、四条边都相等的四边形。
★矩形与正方形:
① 有一个内角是直角的平行四边形叫做矩形。
② 矩形的对角线相等且平分,四个角都是直角。
③ 对角线相等的平行四边形是矩形。
④ 正方形具有平行四边形,矩形,菱形的所有性质。
⑤ 一组邻边相等的矩形是正方形,有一个角是直角的菱形是正方形。
★多边形:
①n 边形的内角和等于(n-2)180°
②多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,他们的和叫做这个多边形的外角和
多边形的外角和都等于 360 度
★加权平均数:一组数据里各个数据的重要程度未必相同,因而,在计算这组数据的平均数时往往给每个数据加一个权,这就是加权平均数。
二、基本定理
其中 x 是 n 个数 x1,x2 … xn 的平均数
1、过两点有且只有一条直线
2、两点之间线段最短
3、同角或等角的补角相等
4、同角或等角的余角相等
5、过一点有且只有一条直线与已知直线垂直
6、直线外一点与直线上各点连接的所有线段中,垂线段最短
7、平行公理 经过直线外一点,有且只有一条直线与这条直线平行
8、如果两条直线都和第三条直线平行,那么这两条直线也互相平行
9、同位角相等,两直线平行
10、内错角相等,两直线平行
11、同旁内角互补,两直线平行
12、两直线平行,同位角相等
13、两直线平行,内错角相等
14、两直线平行,同旁内角互补
15、定理 三角形两边的和大于第三边
16、推论 三角形两边的差小于第三边
17、三角形内角和定理 三角形三个内角的和等于 180°
18、推论 1 直角三角形的两个锐角互余
19、推论 2 三角形的一个外角等于和它不相邻的两个内角的和
20、推论 3 三角形的一个外角大于任何一个和它不相邻的内角
21、全等三角形的对应边、对应角相等
★全等三角形的判定方法:
22、边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
23、角边角公理( ASA)有两角和它们的夹边对应相等的 两个三角形全等
24、推论(AAS) (角角边)有两角和其中一角的对边对应相等的两个三角形全等
25、边边边公理(SSS) 有三边对应相等的两个三角形全等
26、斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等
★角平分线的性质:
27、定理 1 在角的平分线上的点到这个角的两边的距离相等
28、定理 2 到一个角的两边的距离相等的点,在这个角的平分线上
29、角的平分线是到角的两边距离相等的所有点的集合
★等腰(边)三角形的性质:
30、等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角)
31、推论 1 等腰三角形顶角的平分线平分底边并且垂直于底边
32、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(三线合一)
33、推论 3 等边三角形的各角都相等,并且每一个角都等于 60°
★等腰(边)三角形的判定:
34、等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
35、推论 1 三个角都相等的三角形是等边三角形
36、推论 2 有一个角等于 60°的等腰三角形是等边三角形
37、在直角三角形中,如果一个锐角等于 30°那么它所对的直角边等于斜边的一半
38、直角三角形斜边上的中线等于斜边上的一半 。反之如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
★线段垂直平分线的性质:
39、定理 线段垂直平分线上的点和这条线段两个端点的距离相等
40、逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
41、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
42、定理 1 关于某条直线对称的两个图形是全等形
43、定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线
44、定理 3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
45、逆定理 如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称
46、勾股定理 直角三角形两直角边 a、b 的平方和、等于斜边 c 的平方,即 a2 b2=c2
47、勾股定理的逆定理 如果三角形的三边长 a、b、c 有关系 a2 b2=c2,那么这个三角形是直角三角形
48、定理 四边形的内角和等于 360°
49、四边形的外角和等于 360°
50、多边形内角和定理 n 边形的内角的和等于(n-2)×180°
51、推论 任意多边的外角和等于 360°
★平行四边形的性质:
52、平行四边形性质定理 1 平行四边形的对角相等 、邻角互补
53、平行四边形性质定理 2 平行四边形的对边相等 、对边平行
54、推论 夹在两条平行线间的平行线段相等
55、平行四边形性质定理 3 平行四边形的对角线互相平分
★平行四边形的判定:
定义:两组对边分别平行的四边形是平行四边形
56、平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形
57、平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形
58、平行四边形判定定理 3 对角线互相平分的四边形是平行四边形
59、平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形
★矩形的性质:
60、矩形性质定理 1 矩形的四个角都是直角,对边平行且相等
61、矩形性质定理 2 矩形的对角线相等且互相平分
★矩形的判定:
定义:有一个角是直角的平行四边形是矩形
62、矩形判定定理 1 有三个角是直角的四边形是矩形
63、矩形判定定理 2 对角线相等的平行四边形是矩形
★菱形的性质:
64、菱形性质定理 1 菱形的四条边都相等 ,对边平行,对角相等
65、菱形性质定理 2 菱形的对角线互相垂直平分,并且每一条对角线平分一组对角
66、菱形面积=对角线乘积的一半,即 S=(a×b)÷2 ,也等于底×高
★菱形的判定:
定义:一组邻边相等的平行四边形是菱形
67、菱形判定定理 1 四边都相等的四边形是菱形
68、菱形判定定理 2 对角线互相垂直的平行四边形是菱形
★正方形的性质:
69、正方形性质定理 1 正方形的四个角都是直角,四条边都相等 ,对边平行
70、正方形性质定理 2 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角正方形的判定:方法一:是矩形且一组邻边相等
方法二:是菱形且有一个角是直角
71、定理 1 关于中心对称的两个图形是全等的
72、定理 2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
73、逆定理 如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称
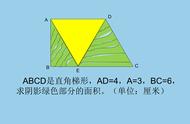
★等腰梯形的性质:
74、等腰梯形性质定理 等腰梯形在同一底上的两个角相等
75、等腰梯形的两条对角线相等
★等腰梯形的判定:
76、等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形
77、对角线相等的梯形是等腰梯形
78、平行线等分线段定理 如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等
79、推论 1 经过梯形一腰的中点与底平行的直线,必平分另一腰
80、推论 2 经过三角形一边的中点与另一边平行的直线,必平分第三边
81、三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半
82、梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半梯形的中位线长=(上底 下底)÷2 梯形面积=中位线长×高
83、平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例
84、推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
85、定理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边
86、平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例
赶快收藏起来吧!