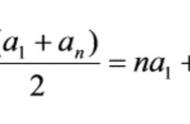小学奥数(第004课) 等差数列求和公式的相应练习题，有兴趣的同学可以做一做。

①心算

1.已知偶数列：2，4，6，8，…，198，200。所有数的和是（ ）。

2.已知一个等差数列所有数的和是99，如果第一项与最后一项的和是33，一共有（ ）项。

3.已知一个等差数列一共有25项，所有数的和是625，那么第3项与第23项的和是 （ ）。

②已知等差数列：12，23，34，45，…一共有99项，那么所有数的和是多少。

③已知等差数列共有77项，所有数的和是13013，如果第二项是21，那么倒数第二项是多少。

④沈阳地铁一号线的一辆列车共有6节车厢，已知后面每一个车厢的人数都比前一个车厢多6人，如果所有车厢的总人数是240，那么第6节车厢有多少人。

⑤小明进行加法珠算练习，用1 4 7 10 13…，当加到某个数时，和是173，在验算时发现重复加了一个数，这个数是多少。

需要PDF打印版，以及想入群学习的可以关注：沈阳奥数。关于小学奥数，育才少儿班有任何疑问或建议也可以联系刘老师，谢谢大家的支持。会陆续为大家奉献精彩内容。以下是答案与解析，供大家参考。

①心算

1.答案：10100

解析：共100项，根据等差数列求和公式：(2 200)×100÷2=101×100=10100

2.答案：6

解析：项数=99×2÷33=3×2=6

3.答案：50

解析：第3项与第23项的和就是首项与末项的和，首项 末项=625×2÷25=25×2=50②答案：54549

解析：公差是11，则第99项：12 (99-1)×11=1090

根据求和公式：(12 1090)×99÷2=54549

或根据公式na1 n(n-1)d/2=99×12 99×(99-1)×11÷2=54549③答案：317

解析：根据求和公式n(a1 an)/2

77×(a1 an)÷2=13013

解得a1 an=338，那么第二项与倒数第二项的和也是338

所以答案是338-21=317④答案：55

解析：车厢1-6的人数构成公差是6的等差数列，设第6项是x，那么第1项是x-(6-1)×6=x-30

根据等差数列求和公式，6(x-30 x)/2=240

解得x=55⑤答案：28

解析：公差是3，设加到第n项。第n项是：1 (n-1)×3=3n-2

不考虑重复的那个数，这些数的和应该是(1 3n-2)n/2=n(3n-1)/2

这里需要估算一下n的大概值，然后再详细确认。

n=10时(末项28)，n(3n-1)/2 = 145 或者(1 28)×10÷2=145

n=11时(末项31)，n(3n-1)/2 = 176 或者(1 31)×11÷2=176

所以答案是173-145=28