七年级开学已经一周多的时间了,学生也慢慢从小学的学习状态向初中转变,对于初中数学,变化还是非常大的,也要改变小学学习数学的思维模式,认真领会数学学习思维,掌握数学思想。

在有理数章节中,数轴这一知识点既是重点也是难点,重点是因为它不单纯是知识点,还是学习其他知识点的工具,是后面学习的基础。难点是因为很多结合数轴或者是利用数轴来解题,利用数形结合思想解题是难点,也是学习的关键。下面就和大家一起来看一种常考题型,就是数轴上两点之间的距离求法。这类题型一般有两种解题思路,下面将会结合具体的实例和大家一起交流分享。

本题来看,数轴已经给出了,并且各点已经明确,利用数形结合思想直接解决就可以了。首先我们先确定原点,根据D和E的距离可得结论。如果点C表示的数是﹣1,则点D表示原点,所以E表示的数是2,故选:D。这类题目比较简单,只需要熟练掌握数轴的性质是解决本题的关键。

这个题目就需要小心了。一个数到一个数的距离是多少,从数轴上我们会知道会有两个,左右各一个。那么思路一:数轴上到一点距离相等的点有两个,分别位于该点的左右,进行分类讨论解答。它们分别是﹣47/6或-5/6.思路二:利用绝对值进行解答,绝对值的定义中我们知道,绝对值表示某个数到原点的距离,因此可以利用绝对值来求解。设这个数为x,则可以列出|x-(-13/3)|=7/2.解这个含有绝对值的方程,根据去绝对值的方法,非常简单,而且这种方法不容易漏解。

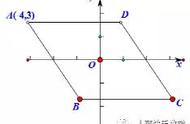
本题是借助数轴,利用数形结合的方法求解。由于点A与原点的距离为3,那么A应有两个点,分别位于原点两侧,且到原点的距离为3,这两个点对应的数分别是﹣3和3。A向右移动4个单位长度,再向左移动7个单位长度,我们可以通过数轴上“右加左减”的规律,即可求得平移后点A表示的数。解答本题的关键是明确数轴的特点,故答案为:﹣6 或 0。

在解答有关数轴上两点之间距离的题目时,最简单的方法就是利用数形结合,但是切记不要漏解,该点左右两边都要考虑到,利用绝对值进行求解不容易漏解,但是很多同学可能会感觉到比较的复杂,但是学好绝对值后,会发现这种方法非常的好用,而且不需要过多的考虑。希望两种方法同学们都能够掌握。