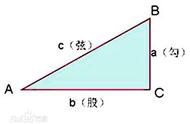
三角形的三个内角和是多少？也许很多人会不假思索地回答：180°。

这个答案作为一个不容置疑的公理伴随了我们整个小学和中学生涯。当我们还在捧着这个公理，认为其放之四海甚至是宇宙都可能皆准的时候，那些学术界的大神的研究已经远远超出了我们的想象，也许很多人都不知道这个世界上还存在三个内角和不等于180°，但这些学术大神已经通过研究证明，这种三角形确实存在，而且还是在我们生活的地球上。

再举一个例子：

拿出世界地图，在上海和巴黎间画条直线。 如果你沿这条线走，会发现自己绕了远路。 先北上再南下，途径莫斯科的线竟然更短。

也就是说两点之间，不是线段最短。

从古希腊时代到公元1800年间，许多数学家都尝试用欧几里得几何中的其他公理来证明欧几里得的平行公理，但是结果都归于失败。19世纪，德国数学家高斯、俄国数学家罗巴切夫斯基、匈牙利数学家波尔约等人各自独立地认识到这种证明是不可能的。也就是说，平行公理是独立于其他公理的，并且可以用不同的“平行公理”来替代它。高斯关于非欧几何的信件和笔记在他生前一直没有公开发表，只是在他1885年去世后出版时才引起人们的注意。

罗巴切夫斯基是从1815年着手研究平行线理论的。开始他也是循着前人的思路，试图给出第五公设的证明。在保存下来的他的学生听课笔记中，就记有他在1816～1817学年度在几何教学中给出的一些证明。可是，很快他便意识到自己的证明是错误的。

前人和自己的失败从反面启迪了他，使他大胆思索问题的相反提法：可能根本就不存在第五公设的证明。于是，他便调转思路，着手寻求第五公设不可证的解答。这是一个全新的，也是与传统思路完全相反的探索途径。罗巴切夫斯基正是沿着这个途径，在试证第五公设不可证的过程中发现了一个崭新的几何世界。

继罗氏几何后，德国数学家黎曼在1854年又提出了既不是欧氏几何也不是罗氏几何的新的非欧几何。这种几何采用如下公理替代欧几里得平行公理：同一平面上的任何两直线一定相交。同时，还对欧氏几何的其他公理做了部分改动。在这种几何里，三角形的内角和大于两直角。人们把这种几何称为椭圆几何。

直到1866年，意大利数学家贝尔特拉米在他出版的《非欧几何解释的尝试》中，证明了非欧平面几何可以局部地在欧氏空间中实现。1871年，德国数学家克莱因认识到从射影几何中可以推导度量几何，并建立了非欧几何模型。这样，非欧几何的相容性问题就归结为欧氏几何的相容性问题，由此非欧几何得到了普遍的承认。