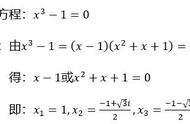我们从两个方面来解读复数的基本概念

一、解读b²-4ac<0的一元二次方程求解的相关知识点

同学们知道在初中解一元二次方程时有一个特殊的情况，当根的判别式b²-4αc<0时没有实数根。实际虽然是没有实数根，但是这个方程也有意义。如果有意义，它是一定有根的。它的根又是什么样子？现在我们就来简要的解读当b²-4ac<0时，一元二次方程根的基本情况。

当b²-4ac<0时，这样的方程，它的根是一个特别的数，这个特别的数叫做复数。

复数的一般形式是"a bⅰ"

即、z=a bⅰ

我们看到复数的一般表达式是一个二项式，而且这个二项式的各项又不是同类项。

注意a，b是实数。"i"是一个记号，它表示ⅰ的平方等于-1的数，即ⅰ²=-1，i不是一个实数。

例如

(1)、2 3ⅰ，(a=2、b=3)

(2)、1/2 √3ⅰ/4，(a=1/2

b=√3/4)

(3)、ⅰ√3，(a=0，b=√3)

(4)、3，(b=0)

当a≠0，b≠0时，这个复数a bi又叫做虚数，虚数仍然是二项式。

当a=0，b≠0时，bi是个单项式，这个单项式bⅰ叫做纯虚数。

例如:2ⅰ，1ⅰ/3等都是纯虚数

当a≠0，b=0时，a是实数。注意，任何实数都可以看做是一个特殊的虚数。

例如、2，4 0i，1ⅰ0/3，0ⅰ√5等都是特殊的虚数

于是我们又懂得了一个道理，在知识网络里，所有的知识点都是互相关联，互相共存的。任何一个知识点，实际都是知识链中的一个不可缺的环节。

下面我们就来解当b²-4ac<0的一元二次方程，它们在实数范围内没有根。但是在复数范围内是有根的，它们的根实际上是一个虚根。

例1、解方程

x² 1=0

ⅹ²=-1

ⅰ²=-1，(-ⅰ)²=-1

x=±ⅰ

例2、解方程

x² 3=0

ⅹ²=-3，-3=-1x3

x=±i√3

我们这是按着实数的规则进行解方程的，要注意当遇到ⅰ²时就可以用-1来表示。

通过解方程，我们还应该知道

b²-4ac<0的一元二次方程确实是有根的，它的根是一个新的数。这个新数就是复数。同时也要看到，我们也是用复数的规则在解一元二次方程。

还应该理解和明确，用复数的加减和乘法的规则进行运算时，只要能够满足i²=-1的一般式就可以。

二、解读复数常用的名词术语

下面我们解读复数中一些常用的名词术语，并且对b²-4ac<0的一元二次方程的根做一个基本的概括。

(1)实部，虚部，虚部系数

在复数a bⅰ中，a叫做实部，

bi叫做虚部，b叫做虚部的系数。

(2)复数是实数的推广

当b=0时，复数a 0ⅰ就是实数。因此复数的集合就包括了实数，所以说实数是一个特殊的复数。复数实际上就是实数的推广，实数是复数的基础。

(3)虚数，存虚数

当a≠0，b≠0时，复数a bi又叫做虚数。

例如、3 2ⅰ，1/2 ⅰ√3等都是

虚数。

当a=0，b≠0时，0 bi叫做纯虚数。

例如、±ⅰ，±i√3等都是纯虚数

(虚数，纯虚数的概念，在上面已经做了解读。再次介绍目的就是加深对虚数，纯虚数的理解和掌握)

(4)共轭复数，

实部相等，虚部系数互为相反的两个复数叫做一个是另一个的共轭复数。

(5)共轭虚数

特别是当复数的虚部系数b≠0时，a bi和a-bi又都是虚数，因此它们互为共轭虚数。

(6)虚数的产生

虚数是历史遗留下来的名称，由于解方程的需要，就把实数扩充到了复数。其实复数没有什么实际意义，它是一个不真实的数，所以我们称它为虚数。后来由于生产和科学的发展，人们逐渐认识到了这类没有实际意义的数，在计算中却有一定的意义。从此虚数被确认为也是一个真实存在的数，并且得到了广泛的研究和应用。

关于复数的基本概念就解读到这里，在解读过程中，有些判断语言是我自己的观点，不一定正确。有错误的地方则以教材为准，也希望审核老师和同学们批评指正。谢谢！