角的计算与证明是人教版七年级上数学考试的重点,刚上初一的同学尤其要注意几何计算与证明的书写格式。下面给出5道与角相关的计算与证明,可以训练一下书写格式。
例1 把一个长方形纸条按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG=_____.
解:∵∠AOB′=70°
∴∠B′OB=180°-70°=110°
∵∠B′OG=∠BOG
∴∠B′OG=∠B′OB÷2=110°÷2=55°
总结:折叠的过程等于在告诉你角平分线。
例2 如图,已知∠BOC=2∠AOC.OD平分∠AOB,且∠COD=19°,求∠AOB的度数。
解:设∠AOC=x
∵∠BOC=2∠AOC
∴∠BOC=2x
∴∠AOB=∠BOC ∠AOC=2x x=3x
∵OD平分∠AOB
∴∠BOD=∠AOB÷2=3x÷2=1.5x
∴∠COD=∠BOC-∠BOD=2x-1.5x=0.5x
∵∠COD=19°
∴0.5x=19°
x=38°
∴∠AOB=3x=114°
总结:有些几何问题转化为代数方法解决,能让过程简洁、明了。
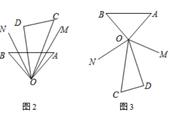
例3 将一副三角板如图放置,OM平分∠AOC,ON平分∠DOC.求∠MON的大小。
解:设∠AOB=x
∵OM平分∠AOC
∴∠COM=∠AOC÷2=15° 0.5x
∵ON平分∠DOC.
∴∠CON=∠DOC÷2=37.5° 0.5x
∴∠MON=∠CON-∠COM=(37.5° 0.5x)-(15° 0.5x)=22.5°
总结:旋转动角问题,设动角为x,用x表示与动角相关的角,并在具体计算中把x抵消是常用方法。
例4如图,已知OB、OC、OD为∠AOE内三条射线。(1)图中共有多少个角?(2)若OB、OC、OD为∠AOE的四等分线,且图中所有锐角的和为400°,求∠AOE的度数;(3) 若∠AOE=89°, ∠BOD=30°,求图中所有锐角的和。
解:(1)1 2 3 4=10(个)
(2)设∠AOB=x
∵图中10个角的和可以求得是20x
∴20x=400⁰
x=20⁰
∴∠AOE=4x=80°
(3)图中10个角的和=∠AOE (∠AOE ∠BCD) (∠AOE ∠BCD) ∠AOE=4∠AOE 2∠BCD
∵∠AOE=89°, ∠BOD=30°
∴图中10个角的和==4×89° 2×30°=416°
总结:计算多个角度的和学会用整体思想
例5 已知O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=30°,求∠DOE的度数
(2)在图1中,若∠AOC=a,求∠DOE的度数
(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置:①探究∠AOC和∠DOE的度数之间的关系;②在∠AOC内部有一条射线OF,满足∠AOC-4∠AOF=2∠BOE ∠AOF,试确定∠AOF和∠DOE的度数之间的关系;说明理由。

解:(1)
∵∠AOC=30°
∴∠BOC=180°-∠AOC=180°-30°=150°
∵OE平分∠BOC
∴∠COE=∠BOC÷2=150°÷2=75°
∵∠COD为直角
∴∠COD=90°
∴∠DOE=∠COD-∠COE=90°-75°=15°
(2)
∵∠AOC=a
∴∠BOC=180°-∠AOC=180°-a
∵OE平分∠BOC
∴∠COE=∠BOC÷2=(180°-a)÷2
∵∠COD为直角
∴∠COD=90°
∴∠DOE=∠COD-∠COE=90°-(180°-a)÷2=0.5a
(3)①设∠COE=m
∵OE平分∠BOC
∴∠COE=∠BOE=m
∴∠AOC=180⁰-∠BOC=180⁰-2m
∵∠COD为直角
∴∠COD=90°
∴∠DOE=∠COD-∠COE=90°-m
∵180⁰-2m=2×(90⁰-m)
∴∠AOC=2∠DOE
②
∵∠AOC-4∠AOF=2∠BOE ∠AOF
∴∠AOC=2∠BOE 5∠AOF
∵OE平分∠BOC
∴∠COE=∠BOE
∴180⁰-∠BOC=2∠BOE 5∠AOF
∴180⁰-2∠COE=2∠COE 5∠AOF
∴180⁰=4∠COE 5∠AOF
∴180⁰=4(90⁰-∠DOE) 5∠AOF
即4∠DOE-5∠AOF=180⁰