第一章 负数的初步认识
1. 0既不是正数,也不是负数。正数都大于0,负数都小于0。
2. 在数轴上,以“0”为分界点,越往左边的负数越小,左边的数都比右边的数小。
3. 在生活中,0作为正、负数的分界点,常常用来表示具有相反关系的量。如零上温度( )、零下温度(—);海平面以上( )、海平面以下(—);盈利( )、亏损(—);收入( )、支出(—);南( )、北(—);上升( )、下降(—)……
4.水沸腾时的温度是100℃,水结冰时的温度是0℃;-10℃比-5℃低5℃,6℃比-6 ℃高12℃。
第二章 多边形的面积
1.一个平行四边形能分割成两个完全相同的三角形;两个完全相同的三角形能拼成一个平行四边形。
2.一个平行四边形可以分割成两个完全相同的梯形;两个不同的梯形也可能拼成一个平行四边形。如图:

3.等底等高的平行四边形的面积相等,周长不等;等底等高的三角形的面积相等,周长不等;一个三角形的面积是与它等底等高的平行四边形面积的一半。
如下图:

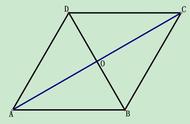
△ADE、△BDE、△BCE面积相等,都是平行四边形BDEC的一半;
△AOD与△BOE的面积相等。想想为什么?
4.把一个长方形框拉成平行四边形,周长不变,高变小,面积也变小;同理,把平行四边形框拉成长方形,周长不变,高变大了,面积也变大。
5.把一个平行四边形拼成长方形,面积不变,宽变小了,周长也变小。

6.要从梯形中剪去一个最大的平行四边形,那么应把梯形的上底作为平行四边形的底,这样剪去才能最大。
7.平行四边形的面积公式的推导(转化法:等积变形):沿平行四边形的任意一条高剪开,移动拼成长方形。长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高。
8.三角形的面积公式的推导:将两个完全一样的三角形拼成一个平行四边形,这个平行四边形的底等于三角形的底,高等于三角形的高,拼成的平行四边形的面积是每个三角形面积的2倍,每个三角形的面积是拼成的平行四边形面积的一半。
9.梯形的面积公式的推导:将两个完全一样的梯形拼成一个平行四边形,这个平行四边形的底等于梯形的上底与下底的和,平行四边形的高等于梯形的高,拼成的平行四边形的面积是每个梯形面积的2倍,每个梯形的面积是拼成的平行四边形面积的一半。
10. 1公顷就是边长100米的正方形的面积,1公顷=10000平方米。1平方千米就是边长1000米的正方形的面积,1平方千米=100公顷=100万平方米=1000000平方米。
11. 一个社区、校园的面积通常用“公顷”为单位;表示一个国家、省市、地区、湖泊的面积是就要用“平方千米”作单位。
12. 农村地区常使用“亩”和“分”作土地面积单位,1亩=10分≈667平方米,1公顷=15亩。
13. 面积单位换算进率:

14.面积计算公式:

组合图形
方法:先用分割、拼补的方法,将组合图形转化成已学的简单图形,分别算出面积;再通过加、减求得。
估算不规则图形
先数整格的,再数不满整格的,不满整格的除以2折算成整格,最后相加;若不规则图形为轴对称图形,可先算出一半图形的面积,再乘以2。
注意:计算前要统一单位,找准对应的底和高,然后代入公式,计算要细心。
第三章 小数的意义和性质
1.分母是10、100、1000……的分数都可以用小数表示。一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……
2.小数的组成:整数部分、小数点和小数部分组成。比较大小时,先比整数部分,再比小数部分。
3.小数数位顺序表

说明:(1)相邻两个计数单位之间的进率都是10;(2)整数部分没有最高位,小数部分没有最低位;(3)整数部分最低位是个位,小数部分最高位是十分位。
4.判断一个小数是几位小数,就是观察小数点后面的数,小数点后面有几个数,就是几位小数。
5.小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。根据小数的性质,可对小数进行化简或按要求改写小数。
6.小数的改写:
(1)用“万”作单位:a、从个位起,往左数四位,画“┆”,在“┆”下方点小数点;b、去掉小数末尾的“0”,添上“万”字;c、用“=”连接。
(2)用“亿”作单位:a、从个位起,往左数八位,画“┆”,在“┆”下方点小数点;b、去掉小数末尾的“0”,添上“亿”字;c、用“=”连接。
7.求整数的近似数:
(1)省略万后面的尾数:看“千”位上的数,用“四舍五入”法取近似值。添上“万”字,用“≈”连接。
(2)省略亿后面的尾数:看“千万”位上的数,用“四舍五入”法取近似值。添上“亿”字,用“≈”连接。
8.求小数的近似数:
(1)保留整数:就是精确到个位,要看十分位上的数来决定四舍五入。
(2)保留一位小数:就是精确到十分位,要看百分位上的数来决定四舍五入。
(3)保留两位小数:就是精确到百分位,要看千分位上的数来决定四舍五入。