（本来想在中午发的基础上修改的，结果是修改内容太多，只能重新完整发一次，占用资源，见谅。）

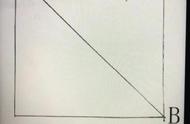
题目其实不难，难在怎样让小学生找到这个题目中各种图形的特点，有正方形、梯形、三角形，把这些特点分析分析，就会找到不止一种方法。

解法一：

（思路）直观解题方法。阴影部分面积就是直角梯形ABCE的面积减去△ABF、△CEF的面积，因此只要求出两个对角相似三角形的面积就行了。而要求面积，我们就要知道底和高，底我们知道，分别是5和15，那么我们先来找出高。

很多符号这里显示不了，还没有研究好，只好用图了。

今天有点忙，先上一种解法，晚上再上一种，看看有没有条友有其他好的方法的。

解法二：

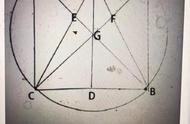
连接D，F并延长交BC于G。设△CFE的面积为S。

∵AC为正方形ABCD的对称轴，BC，CD是以AC为对称轴的对称边，则CG=CE，

△CFG≌△CFE，△BCE≌△DCG。

∴S△CFG=S△CFE=S。

∵△CFE与△DFE底边CD上高相等，且DE=2CE，

∴S△DFE=2S，S△CDG=S△CBE=4S，S△CBF=S△CBE=（CEBC）

=（515）

=

同时，根据三角形同底等高可知：S△ABE=S△ABC，S△AFE=S△CBF

∴S阴影=2 ==

解法三：

（思路：直接求阴影部分面积，要找出底和高的值。）

根据三角形同底等高可知：S△ABE=S△ABC，S△AFE=S△CBF

由E点作EH⊥AC，则△CEH为等腰RT△。

∴EH=

∵AB∥CE，∴∠ABF=∠FEC，∠BAF=∠FCE，而∠AFB=∠CFE

∴△ABF∽△CEF

∵AB=15=3CE，∴AF=3CF

∵正方形边长为15，则对角线AC=15

∴AF=AC=

∴S△AFE=AFEH==

∵S△AFE=S△CBF

∴S阴影=2S△AFE=

可能还有别的解题方法，请条友指教。