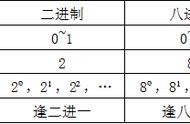
二进制与十进制表
十进制数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二进制数 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
十进制数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
二进制数 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 | 10011 | 10100 |
十进制数 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
二进制数 | 10101 | 10110 | 10111 | 11000 | 11001 | 11010 | 11011 | 11100 | 11101 | 11110 |

二进制与十进制表
位运算符
位操作是程序设计中对位模式按位或二进制数的一元和二元操作。
运算符 | 描述 | 例子 | 类似于 | 结果 | 十进制 |
& | AND,按位与处理两个长度相同的二进制数,两个相应的二进位都为 1,该位的结果值才为 1,否则为 0。 | x = 5 & 1 | 0101 & 0001 | 0001 | 1 |
| | OR,按位或处理两个长度相同的二进制数,两个相应的二进位中只要有一个为 1,该位的结果值为 1。 | x = 5 | 1 | 0101 | 0001 | 0101 | 5 |
~ | 取反,取反是一元运算符,对一个二进制数的每一位执行逻辑反操作。使数字 1 成为 0,0 成为 1。 | x = ~ 5 | ~0101 | 1010 | -6 |
^ | 异或,按位异或运算,对等长二进制模式按位或二进制数的每一位执行逻辑异按位或操作。操作的结果是如果某位不同则该位为 1,否则该位为 0。 | x = 5 ^ 1 | 0101 ^ 0001 | 0100 | 4 |
<< | 左移,把 << 左边的运算数的各二进位全部左移若干位,由 << 右边的数指定移动的位数,高位丢弃,低位补 0。(相当于乘以2的幂次方) | x = 5 << 1 | 0101 << 1 | 1010 | 10 |
>> | 右移,把 >> 左边的运算数的各二进位全部右移若干位,>> 右边的数指定移动的位数。(相当于除以2的幂次方,结果取整数) | x = 5 >> 1 | 0101 >> 1 | 0010 | 2 |
>>> | 无符号右移,与有符号右移位类似,除了左边一律使用0 补位。 | x = 2 >>> 1 | 0010 >>> 1 | 0001 | 1 |
>> 是指有符号位移。 (简单理解就是区分一个数字的正负在进行移动)。
>>> 是指无符号位移。 (简答理机就是会无视一个数字是正数还是负数,进行统一规则的运算)。
10 的 二进制是 1010
10 >> 1 // 5
10 >>> 1 // 5
10 的二进制是 1010,所以向右移动一位,就是 101,右边移动一位,所以为了补全32位(四个字节),就需要参照,正数前面补充0,负数补充1的规则,然后十进制表示就是 5,0000..000(29个零)101。
正数以二进制容易表示,负数在计算机中是以(补码 = 反码 1)。
-10用补码表示
二进制 000...000(28个0)1010
反码 111...111(28个1)0101
补码 111...111(28个1)0110
-10 >> 1
有符号位移的话,
右边移去了一个0,111...111(28个1)011,
前面补1,得到 111...111(29个1)011
在存放整数的存储单元中,最左面的一位是符号位:该位为0,表示数值为正;该位为1,表示数值为负。
所以我们继续求回原码。第一位是 "0" 的是正数,正数的原码就是补码。如果补码的符号位为“1”,表示该数是一个负数,那么对给定的这个补码再求补码,就是要求的原码。
我们上面求补码的方法是先取反在 1,现在我们继续对上面求的补码进行取反。
第一位的 0 表示该数是一个负数,所以不变更符号位,该位仍为“1”。
对除符号位以外的数值位取反,结果为 1000...000(28个0)100。
对上面的取反后的值 1,得到 1000...000(28个0)101。
我们将除去第一位的1, 然后其他位 000...000(28个0)101 求十进制,得到 5,加上第一位的符号位,得到 -5。
-10 >>> 1
无符号位移的话,
右边去掉一个0,111...111(28个1)011,
左边补充一个0(无视正,负),0111...111(28个1)011,
然后正数的十进制表示出来 0111..111(28个1)011 十进制变成 2147483643。