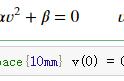今天要讨论的是一类相对容易求解的微分方程──二阶常系数齐次线性微分方程。
我们拿到一个二阶常系数齐次线性微分方程
y" py' qy=0 微分方程(1)
(其中p和q都是常数),想要求其通解。由二阶齐次线性微分方程的解的结构,我们知道:如果能找到此微分方程两个线性无关的解y₁和y₂,那么y=C₁y₁ C₂y₂即是其通解(C₁和C₂为任意常数,下同)。
我们知道函数y=eʳˣ (r为常数)的各阶导数之间都只相差一个常数因子,这个特性非常适合微分方程(1)的胃口。因而我们有理由做这样一个猜测:是不是能找到一个合适的常数r使得y=eʳˣ满足微分方程(1)。在这种猜测下,我们试着把y=eʳˣ代入到微分方程(1)中,整理得
(r² pr q)eʳˣ=0
因为eʳˣ≠0,所以
r² pr q=0 方程(2)
只要r满足方程(2),y=eʳˣ便是微分方程(1)的一个解。我们把方程(2)叫做微分方程(1)的特征方程。
特征方程r² pr q=0的根可能有三种情况,这也导致微分方程(1)的通解有三种不同情形,我们分别讨论:
(一)若p²-4q>0,特征方程有两个不相等实根r₁和r₂,那么
y=C₁eʳ¹ˣ C₂eʳ²ˣ
便是微分方程(1)的通解。
(二)若p²-4q=0,特征方程有两个相等实根r₁=r₂,那么y₁=eʳ¹ˣ便是微分方程(1)的一个解。要想求微分方程(1)的通解还需找到一个与y₁线性无关的解。这就又到了关键时刻,需要我们大胆推测另外一个解的形式y₂=u(x)y₁=u(x)eʳ¹ˣ,其中u(x)是x的函数,且u(x)≠常数。当我们把y₂=u(x)eʳ¹ˣ代入到微分方程(1)中整理发现,只要u(x)的二阶导数等于0就能使得微分方程(1)成立。那么我们不妨选u(x)=x,于是y₂=xeʳ¹ˣ,这样就可以得到微分方程(1)的通解:
y=C₁eʳ¹ˣ C₂xeʳ¹ˣ=(C₁ C₂x)eʳ¹ˣ
(三)若p²-4q<0,特征方程有一对共轭复根r₁=a bi,r₂=a-bi (b≠0)。那么eʳ¹ˣ和eʳ²ˣ便是微分方程(1)的两个解,但它们是复值函数形式。我们希望得到实值函数形式的解,我们利用欧拉公式eⁱᵇ=cos b isin b和齐次线性微分方程解的叠加原理得到微分方程(1)的两个实值函数形式的解:
y₁=(eʳ¹ˣ eʳ²ˣ)/2=eᵃˣcos bx
y₂=(eʳ¹ˣ-eʳ²ˣ)/2i=eᵃˣsin bx
于是,得到微分方程(1)的通解:
y=C₁eᵃˣcos bx C₂eᵃˣsin bx
=eᵃˣ(C₁cos bx C₂sin bx)
如上,只要求得二阶常系数齐次线性微分方程的特征方程的根,就能轻松得到该微分方程的通解。
以上为个人理解。如有错误,欢迎指正。