高等数学对老黄这样的一般人来说,实在是太难了,但对天才来说,可能就没有那么难吧。老黄本也有机会成为“天才”,只可惜浪费了太多时间,终成了一个碌碌无为的庸才,所以告诉年轻人一声,你现在还有成为天才的可能,千万不要放弃哦。

下面这道关于泰勒公式的应用题,对老黄来说,能够看懂已经是极限了,但老黄却还要努力突破极限,不仅要看懂,还要把它解析出来,让爱学习,想成为天才的小伙伴们,也能看懂,想明白,并内化为自己的知识。当然,后面的环节老黄就帮不了你,需要你自己的努力了。
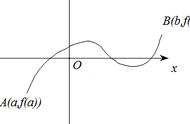
设函数f在[a,b]上二阶可导,f’(a)=f’(b)=0, 证明:
存在一点ξ∈(a,b),使得|f”(ξ)|≥4/(b-a)^2 *|f(b)-f(a)|.
分析:看到这个结论,第一反应其实是应用拉格朗日中值定理,而且要用到两次拉格朗日定理。只可惜,老黄试过之后,发现仅在[a,(a b)/4]上,用拉格朗日定理可以推出这个结论。而在[a,b]的其它子区间上,最多能推出|f”(ξ)|≥2/(b-a)^2 *|f(b)-f(a)|. 即式子中的系数“4”被缩小了,这显然是不能接受的。
假如你只需要运用拉格朗日定理就能推导出这个结论的话,老黄要拜你为师。那不一定是不可能的哦,只是老黄太笨做不到而已。后来老黄也尝试过柯西中值定理,不出意料,也是铩羽而归。最后无路可走的老黄偷瞄了一下答案,才知道,这个问题要用泰勒公式的定量形式,即带拉格朗日余项的泰勒公式形式来解决。不过你千万不要以为,方向找到了,后面的问题就顺理成章,变得很容易了哦。事实上,后面的证明过程依然荆棘满路。
这里的泰勒公式只须取一阶就够了。关于泰勒公式的内容,请详看《老黄学高数》系列视频第185-195讲的内容,重点在第191讲。
证:f(x)=f(a) f’(a)(x-a) 1/2*f”(ξ1)(x-a)^2=f(a) 1/2*f”(ξ1)(x-a)^2, a<ξ1<x, 【这是f(x)在x0=a的一阶泰勒公式,这里称它为“a公式”】
f(x)=f(b) f’(b)(x-b) 1/2*f”(ξ2)(x-b)^2=f(a) 1/2f”(ξ2)(x-b)2, x<ξ2<b, 【这是f(x)在x0=b的一阶泰勒公式,这里称它为“b公式”。】
f((a b)/2)=f(a) f”(ξ1)(b-a)^2/8,a<ξ1<(a b)/2, 【这是a公式在x=(a b)/2的函数值】
f((a b)/2)=f(b) f”(ξ2)(b-a)^2/8, (a b)/2<ξ2<b,【这是b公式在x=(a b)/2的函数值,之所以知道要取泰勒公式的这四个形式,都是运用拉格朗日中值定理过程中,提炼出来的。所以你最好自己用拉格朗日中值定理试几试,就会有所发现】
f((a b)/2)-f(a)=f”(ξ1)(b-a)^2/8, f((a b)/2)-f(b)=f”(ξ2)(b-a)^2/8, 【这是上面两个式子的变形,因为下面要用到,先化成这个形式,会更直接】
取|f”(ξ)|=max{|f”(ξ1)|,|f”(ξ2)|}, 则ξ∈(a,b),【这一步很简单,但它是全题的核心】
|f(b)-f(a)|≤|f(b)-f((a b)/2)| |f((a b)/2)-f(a)|=(|f”(ξ1)| |f”(ξ2)|)(b-a)^2/8≤|f”(ξ)|(b-a)^2/4. 【一般的想法会直接代入f(b)和f(a)的表达式,但那样可能推导不出最后的结论。这里运用的是绝对值的三角不等式】
∴|f”(ξ)|≥4/(b-a)^2 *|f(b)-f(a)|. 得证!

如果你只看过程,不会发现它的困难之处的,但自己尝试证明或者理解证明过程,你就会发现它的难点了。你觉得呢?
,