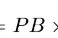一、整数和小数
1.最小的一位数是1,最小的自然数是0
2.小数的意义:把整数“1”平均分成10份、100份、1000份……这样的一份或几份分别是十分之几、百分之几、千分之几……可以用小数来表示。
3.小数点左边是整数部分,小数点右边是小数部分,依次是十分位、百分位、千分位……
4.整数和小数都是按照十进制计数法写出的数。
5.小数的性质:小数的末尾添上0或者去掉0,小数的大小不变。
6.小数点向右移动一位、二位、三位……原来的数分别扩大10倍、100倍、1000倍…… 小数点向左移动一位、二位、三位……原来的数分别缩小10倍、100倍、1000倍……
二、数的整除
1.因数和倍数:20÷4=5,20是4和5的倍数,4和5是20的因数。
2.一个数倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。 一个数因数的个数是有限的,最小的因数是1,最大的因数是它本身。
3.能被2整除的数叫做偶数,不能被2整除的数叫做奇数。
4.质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数。质数都有2个因数。 合数:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。合数至少有3个因数。 最小的质数是2,最小的合数是4 1~20以内的质数有:2、3、5、7、11、13、17、19 1~20以内的合数有“4、6、8、9、10、12、14、15、16、18
5.能被2整除的数的特征:个位上是0、2、4、6、8的数,都能被2整除。 能被5整除的数的特征:个位上是0或者5的数,都能被5整除。 能被3整除的数的特征:一个数的各位上数的和能被3整除, 这个数就能被3整除。
6.公约因数、公倍数:几个数公有的因数,叫做这几个数的因数;其中最大的一个,叫做这几个数的最大公因数。 几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
7.互质数:公因数只有1的两个数叫做互质数。
三、四则运算
1.一个加数=和-另一个加数 被减数=差 减数 减数=被减数-差 一个因数=积÷另一个因数 被除数=商×除数 除数=被除数÷商
2.在四则运算中,加、减法叫做第一级运算,乘、除法叫做第二级运算。
3.运算定律:
(1)加法交换律:a b=b a 两个数相加,交换加数的位置,它们的和不变。 乘法交换律:a×b=b×a 两个数相乘,交换因数的位置,它们的积不变。
(2)加法结合律:(a b) c=a (b c) 三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。 乘法结合律:(a×b)×c=a×(b×c)三个数相乘,先把前两个数相乘,再同第三个数相乘;或者先把后两个数相乘,再同第一个数相乘,它们的积不变。
(3)乘法分配律:(a b)×c=a×c b×c两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
(4)减法的性质:a-b-c=a-(b c) 从一个数里连续减去两个数,等于从这个数里减去两个减数的和。 除法的性质:a÷b÷c=a÷(b×c)一个数连续除以两个数,等于这个数除以两个除数的积。
四、关系式
1.行程问题: 速度×时间=路程 路程÷时间=速度 路程÷速度=时间
2.工作分配问题: 工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率
3.价格问题: 单价×数量=总价 总价÷数量=单价 总价÷单价=数量
五、方程方程:含有未知数的等式叫做方程。方程的解:使方程左右两边相等的未知数的值,叫做方程的解。解方程:求方程解的过程叫做解方程。
六、分数和百分数
1.分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。 分数单位:把单位“1”平均分成若干份,表示其中一份的数,叫做分数单位。
2.分数和除法的*分数的分子就是除法中的被除数,分母就是除法中的除数。
3.分数和小数的*小数实际上就是分母是10、100、1000……的分数。
4.分数和比的*分数的分子就是比的前项,分数的分母就是比的后项。
5.分数的分类:分数可以分为真分数和假分数。 真分数:分子小于分母的分数叫做真分数。真分数小于1。 假分数:分子大于或等于分母的分数叫做假分数。假分数大于或者等于1。
6.最简分数:分子与分母互质的分数叫做最简分数。
7.分数的基本性质:分数的分子和分母同时乘或除以相同的数(零除外),分数的大小不变。8.这样的分数可以化成有限小数:前提是这个分数要是最简分数,如果分母只含有2、5这2个质因数,这样的分数就能化成有限小数。
9.百分数:表示一个数是另一个数的百分之几的数叫做百分数。百分数也叫做百分率或者百分比。百分数通常用“%”来表示。
七、量的计量
1.长度单位有:千米、米、分米、厘米、毫米,写出它们之间的进率:
面积单位有:平方千米、公顷、平方米、平方分米、平方厘米,写出它们之间的进率:
体积(容积)单位有:立方米、立方分米(升)、立方厘米(毫升),写出它们之间的进率: 。
质量单位有:吨、千克、克,写出它们之间的进率: 。
时间单位有:世纪、年、月、日、时、分、秒,写出它们之间的进率: 。
2.一年中的大月有:1、3、5、7、8、10、12月,共7个,每月31天。 小月有:4、6、9、11月,共4个,每月30天。 二月平年是28天,闰年是29天。 左拳记月法
3.一年有4个季度(春、夏、秋、冬),每个季度3个月。
4.平年闰年:公历年份是4的倍数的一般是闰年,公历年份是整百数的,必须是400的倍数才是闰年。
5.名数:把计量得到的数和单位名称合起来叫做名数。 单名数:只带有一个单位名称的叫做单名数。如4千克 复名数:带有两个或两个以上单位名称的叫做复名数。如4千克250克
6.名数的改写:高级单位的名数化成低级单位的名数乘进率,低级单位的名数化成高级单位的名数除以进率。
八、几何初步知识
1.线段、射线、直线的联系与区别:联系是三者都是直的,区别是线段有两个端点,可以量出长度;射线只有一个端点,可以无限延长;直线没有端点,两端都可以无限延长。射线和直线是无限长的。
2.角:从一点引出两条射线所组成的图形叫做角。
3.角的大小:角的大小看两条边张开的大小,张开的越大,角越大。 计量角的大小的单位:度,用符号“°”表示。 小于90°的角叫做锐角;大于90°而小于180°的角叫做钝角。角的两边在一条直线上的角叫做平角。平角180°。
4.垂线:两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。(画图说明)
5.平行线:在同一平面内不相交的两条直线叫做平行线。也可以说这两条直线互相平行。
6.(画图说明)平行线之间垂直线段的长度都相等。
7.三角形:有三条线段围成的图形叫做三角形。8.三角形的分类:(1)按角分:锐角三角形(3个角都是锐角)、钝角三角形(有1个角是钝角)、直角三角形(有1个角是直角)。(2)按边分:一般三角形、等腰三角形(2条边长度相等)、等边三角形(3条边长度相等)。
9.三角形三个内角和是180°。三角形任意两边之和大于第三边。
10.四边形:由四条线段围成的图形。
11.圆是一种曲线图形。圆上任意一点到圆心的距离都相等,这个距离就是圆的半径的长。
12.圆的半径、直径都有无数条。在同一个圆里,直径是半径的2倍,半径是直径的二分之一。
13.轴对称图形:如果一个图形沿着一条直线对折,直线两侧的图形能够完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
14.学过的图形中的轴对称图形有:
圆(无数条)、等腰三角形(1条)、等边三角形(3条)、
长方形(2条)、正方形(4条)、等腰梯形(1条)
15.周长:围成一个图形的所有边长的总和就是这个图形的周长。 面积:物体的表面或围成的平面图形的大小,叫做它们的面积。
16.表面积:立体图形所有面的面积的和,叫做这个立体图形的表面积。 体积:物体所占空间的大小叫做物体的体积。
17.长方体、正方体都有12条棱,6个面,8个顶点。 正方体是特殊的长方体,等边三角形是特殊的等腰三角形。
18.圆柱的三个特点:
(1)上下一样粗细;(2)侧面是曲面;(3)两个底面是相同的圆。
19.圆柱的高:圆柱两个底面之间的距离叫做圆柱的高。圆柱的高有无数条,这些高都平行且相等。
20.把圆柱的侧面展开,得到一个长方形,这个长方形的长等于圆柱的底面的周长,宽等于圆柱的高。
21.圆周率π是一个无限不循环小数。π=3.141592653……
22.把圆等份成若干份,拼成的图形接近于长方形。这个长方形的长相当于圆周长的一半,宽就是圆的半径。
23.圆锥的高:从圆锥的顶点到底面圆心的距离是圆锥的高。
24.等底等高的圆锥的体积是圆柱的,等底等高的圆柱的体积是圆锥的三倍。
九、比和比例
1.比的意义:两个数相除又叫做两个数的比。
2.求比值:比的前项除以比的后项所得的商叫做比值。
3.比的基本性质:比的前项和后项都乘或除以相同的数(0除外),比值不变。
4.应用比的基本性质可以化简比;
5.用字母表示比与除法和分数的关系。 a:b=a÷b=(b≠0)
6.比例尺:我们把图上距离和实际距离的比,叫做这幅图的比例尺。
7.图上距离:实际距离=比例尺 实际距离=图上距离÷比例尺
图上距离=实际距离×比例尺
8.求比值的方法:根据比值的意义,用前项除以后项,结果是一个数。 化简比的方法:根据比的基本性质,把比的前项和后项都乘或除以相同的数(0除外),结果是一个最简整数比。9.正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。用式子表示x:y=k(一定),用图表示正比例关系是一条直线。
10.反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。用式子表示:xy=k(一定),用图表示反比例关系是一条曲线。
十、简单的统计
1.常见的统计图有条形统计图、折线统计图和扇形统计图。
2.条形统计图特点:
(1)用一个单位长度表示一定的数量。
(2)用直条的长短来表示数量的多少。
作用:从图中能清楚地看出各数量的多少,便于相互比较。
折线统计图的特点:
(1)用一个单位长度表示一定的数量。
(2)用折线的起伏来表示数量的增减变化。
作用:从图中能清楚地看出数量的增减变化情况,也能看出数量的多少。
扇形统计图的特点:能清楚地看出各部分与整体之间的关系。
十一、实验公式的整理
(一)平面图形:
1.长方形: 周长=(长 宽)×2 C长=(a b)×2 面积=长×宽 S长=a×b
2.正方形: 周长=边长×4 C正=a×4 面积=边长×边长 S正=a×a
3.平行四边形的面积=底×高 S平=ah
4.三角形的面积=底×高÷2 S三=ah÷25.梯形的面积=(上底 下底)×高÷2 S梯=(a b)×h÷26.圆的周长=直径×3.14 C圆=πd 圆的周长=半径×2×3.14 C圆=2πr 圆的面积=半径的平方×圆周率 S圆=πr2
十二、立体图形:
1.长方体 棱长和=(长+宽+高)×4
L长=4(a+b+h)
表面积=(长×宽 长×高 宽×高)×2
S长表=(ab ah bh)×2
体积=长×宽×高 V长=abh
2.正方体 棱长和=边长×12
L正=12a 表面积=棱长×棱长×6 S正表=a×a×6 体积=棱长×棱长×棱长 V正=a33.圆柱 侧面积=底面周长×高 表面积=侧面积 两个底面积 体积=底面积×高4.以上立体图形的表面积、体积可以统一成公式为: 表面积=底面周长×高 两个底面积
体积=底面积×高 侧面积=底面周长×高
5.圆锥的体积=圆柱的体积÷3 V锥=1/3sh