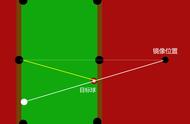
打台球时，遇到下图球形，我们选择翻袋进球。所谓翻袋，是指目标球撞击库边以后，被库边反弹进袋。下面仅讨论翻袋时，入射角等于反射角的理论理想模型。目标球撞击库边的力度以及目标球自带旋转，都会对反射角造成影响。找到理想撞击库边假想点，再根据自身的击球特点，修正后找到属于自己的实际撞击库边假想点，以达到进球目的。

首先，先建立简化三维模型。目标是：白求击中黑球后，黑球撞击库边，然后反弹进袋

.

下面论证一库翻袋的两种理想库边撞击点的寻找方法。

方法：点A为目标球中心，直线P1P2距离库边半颗球，作点A1关于直线P1P2对称。直线A1P与直线P1P2相交于点O。则点O为理想撞击库边假想点。

论证：作直线OM平行于直线AA1,

根据同位角相等，易知角POM=角PA1A，

根据内错角相等，易知角AOM=角OAA1，

再等腰三角形中，易知角OAA1=角PA1A，

得，角POM=角PA1A=角OAA1=角AOM，

所以，角POM=角AOM，证毕！

方法：点A为目标球中心，直线P1P2距离库边半颗球。作直线AP2垂直于直线P1P2。点M为直线AP1与直线PP2的交点。过点M作直线P1P2的垂线交直线P1P2于点O。则点O为理想撞击库边假想点。

论证：根据三角形相似判定定理，一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。相似三角形对应边成比例，则有

三角形P1OM与三角形P1P2A相似，得P1O/P1P2=OM/P2A.......①,

三角形P2OM与三角形P2P1P相似，得P2O/P1P2=OM/P1P........②,

①/②得，P1O/P2O=P1P/P2A,又角PP1O=角AP2O,则

三角形AP2O与三角形PP1O相似，则

角OAP2=角OPP1,

又因，角OAP2=角AOM,角OPP1=角POM,

所以，角AOM=角POM,证毕！

值得注意的是，找到O以后，有自然就确定了点O2和点O3，点O3同样可以作为翻袋时的理想撞击库边假想点。