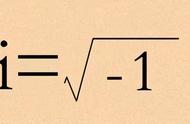虚数单位“i”是数学中非常重要的一个概念。它最初被定义为 $\sqrt{-1}$，看上去似乎毫无意义。但随着数学和物理学的发展， “i”在各种领域都有着重要的应用，帮助了我们更好地理解和解决各种问题。

虚数是由实数乘以虚数单位“i”得到的数。虚数的一般形式为 a bi，其中 a 是实部，b 是虚部。实数可以看做虚部为 0 的虚数。

实际上， “i”本身并不是实数，而是虚数。虚数是一种非实数（也称为复数），它具有实部和虚部。在复数系中，存在着实数和虚数两种基本元素，它们共同组成了复数。事实上，所有实数都可以视为具有零虚部的复数。

虚数在复平面上表示为一个点，其实部与横轴的投影表示为点的横坐标，虚部与纵轴的投影表示为点的纵坐标。因此，虚数 a bi 在复平面上对应的点的坐标为(a,b)。下面是一个虚数在复平面上的示意图：

复数的四则运算和实数的运算类似，具体如下：

复数的加法和乘法满足交换律和结合律，但是并不满足除法的交换律和结合律。

例如，将两个复数相加时，只需要把这两个复数实部分别相加，虚部分别相加即可。同样，将两个复数相乘时，只需要按照二次方程的求根公式进行计算即可。

欧拉公式是数学中一条重要的公式，它表示为：