一、找规律填数:179,278,377,476, , ,773,872
二、下面的数列具有一定的规律,找规律在口里填上适当的数
1,3,8,16,27,□,58
三、 观察分析各列数的规律,然后填空.
(1)3 , 6,12, 24, ,96,192,……
(2)0,1, 3 , 6 , 10, 15 , , 28,……
四、计算:202-204-206 208 210-212-214 216 … 2002-2004-2006 2008=
五、计算 : (1 2 3 … 2008 2009 2008 --- 3 2 1)÷2009=
六、已知六个数按以下顺序排列:2,3,5,9,17,33,…,如此继续排下去,第七、八个数是什么?
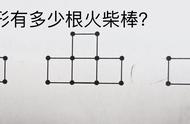
七、如下图所示,用火柴棒横着排正方形,如果使用70根火柴棒,那么可排出 个正方形。……
八、下图是蜂巢的一部分,假如从中间到外面有4层,每个小正六边形中有一只幼蜂,那么这个蜂巢里共有 只幼蜂。
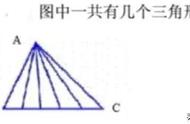
九、3根火柴棒可以摆成一个小三角形,用很多根火柴棒摆成了一个如下图那样的大三角形,如果大三角形外沿的每条边都增加到10根火柴棒,那么摆成这样形状的大三角形需要 根火柴棒。
十、在下图□里填上符合规律的数。
十一、下图是一个用火柴棒摆成的由若干个正六边形组成的图形,若要由里到外摆4圈(在图片的基础上再加两圈),那么一共需要 根火柴棒。
十二、小张将一些同样大小的正方形纸片摆放在桌上.第一次在桌子中间放1个纸片(如图(l));第二次在这个小正方形纸片四周再放一圈纸片(如图(2));第三次在第二次摆放的图形外再放一圈纸片(如图(3))…….她按此规律共摆了十次,那么她共用了正方形纸片 个图(1) 图(2) 图(3)
A.100 B.144 C.181 D.196 E.200
十三、如下图所示,白色和黑色的三角形按顺序排列,当两种三角形的数量相差12个时,白色三角形有____个,
十四、有一张纸,第一次把它剪成7块;第二次从第一次所得的纸片中任取一块,再剪成7块;第三次再从前面所得的所有纸片中任取一块,再剪成7块……这样进行下去,问第10次剪完后,剪出来的纸片共多少块?是否有可能在某一次剪完后,所有纸片的数量正好是2010?为什么?
十五、张杰从27起写了26个连续奇数,王强从26起写了26个连续自然数,然后他们分别将自己写的26个数求和,那么这两个和的差是
十六、在下面的一列数中,从左向右数,第8个数是 .
1,4,10,20,35,…,
十七、学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行,如图所示。现在阅览室做了146人,那么阅览室中拼成一行的方桌有 张。
十八、一台计算机感染了病毒,在计算机的存储器中,从2到9的每一个数x被1 2 3 .... x的和代替,例如2被3(3=1 2)代替,5被15(15=1 2 3 4 5)代替。计算机的其他性能都正常。你若要计算1 3 5,计算机会显示的结果是
十九、从2003中减去215以后,再加上212,然后再减去以215,再加上212......这样不断循环,那么减到 次得数为0。
二十、计算:1-(1 2) (1 2 3)-(1 2 3 4) ........-(1 2 ....... 98) (1 2 ....... 99)
=
二十一、观察下图中数字排列的特点,根据此特点可知△、☆、※所代表数字之和是。
二十二、下面的算式是按一定的规律排列的:4 2,5 8,6 14,7 20,.......,那么和为83的算式是
二十三、如下图所示,小正方形的边长是1厘米,依次作出下面图形
上图第一个图形的周长是10厘米,那么,由36个正方形组成的图形周长是 厘米
二十四、有一组算式:1 1 1,2 3 4,3 5 7,4 7 10,5 9 13,6 11 16,7 13 19,…,那么第2005个算式中三数的和是
二十五、有许多等式:2 4 6=1 3 5 3
8 10 12 14=7 9 11 13 4
16 18 20 22 24=15 17 19 21 23 5
第10个等式右边的和是__ __
二十六、有若干根长度相等的火柴棒,把这些火柴棒摆成下面的图形,照这样摆下去,摆到第10个图,一共用了 根火柴棒.
二十七、一个六角形的花坛的周围用三角形和正方形的砖块铺路(见下图),从花坛中心向外共铺八层,则铺设整个路面所用的三角形和正方形砖块总数是 块.
二十八、3根火柴棒可以摆成一个小三角形,用很多根火柴棒摆成了下图那样的一个大三角形,如果大三角形外沿的每条边都增加到10根火柴棒,那么摆成这样形状的大三角形共需要__ __根火柴棒,
二十九、下面的各算式是按规律排列的:1 1,2 3,3 5,4 7,1 9,2 11,3 13,4 15,1 17,…,那么第18个算式是 ,其中第 个算式的结果是1992。
三十、编号是1、2、3、…、36号的36名学生按编号顺序面向里站成一圈,第一次,编号是1的同学向后转,第二次,编号是2、3的同学向后转,第三次,编号是4、5、6的同学向后转,……,第36次,全体同学向后转.这时,面向里的同学还有 名
三年级思维训练4--找规律
参考答案
1、答案:575,674
分析:方法一:相邻两项差为99,所以两个空分别为575,674.
方法二:分别观察每个数的百位、十位、个位,
百位:1,2,3,4,….
十位:7,7,7,7,….
个位:9,8,7,6.….
很容易得出应填575,674.
2、答案:41
分析:该数列的规律为,每两个相邻的数相差为2,5,8,11,14,17,所以□里面的数为27 14=41
3、答案(1)48
(2)21
分析:(1)后一个数是前一个数的2倍,因此由24X2或96÷2得到48
(2)相邻两数的差组成的数列是1,2,3,4,5,6,....,则15 6得到21
4、答案:0
分析:原式=(202-204-206 208) (210-212-214 261) ..... (2002-2004-2006 2008)=0
5、答案:2009
分析:通过等差数列求和得到1 2 3 ..... (n-1) n (n 1) ..... 3 2 1=n2
(1 2 3 ... 2008 2009 2008 ... 3 2 1)÷2009=20092÷2009=2009
6、答案:65,129
分析:相邻两项差依次为1,2,4,8,16,...,所以第七个数为33 32=65,第八个数为65 64=129
7、答案:23
分析(70-1)÷3=23
8、答案:37
分析:共1 6 12 18=37只
9、答案:165
分析:所有火柴棒共有三种方向:“/”、“\”和“—”。
因为三个方向数量相同,大三角形的火柴棒数量为(1 2 3 ... 10)×3=165(根)
10、答案:4,4,10,10
分析:规律为:下面的数为上面两个数之和,所以□里面填4、4、10、10
11、答案:210
分析:正中间的黑六边形需要6根;加上第一圈之后,增加了(1 3)×6=24(根);加上第二圈之后,增加了(2 5)×6=42(根);观察到6,24,42形成公差为18的等差数列,所以这个规律可以递推.四圈就是该 等差数列的前5项之和,等于42×5=210.
12、答案:C
分析:第2个图形比第1个图形多4×1=4(个),第3个图形比第2个图形多4×2=8(个),第4个图形比第3个图形多4×3=12(个),……,第10个图形比第9个图形多4×9=36(个).第10个图形共有1 4 8 12 ... 36=181(个).选C.
13、答案:66
分析:黑色三角形数:1,(1 2),(1 2 3),(1 2 3 4),…白色三角形数:0,1,(1 2),(1 2 3),…差:1,2,3,4,…当差为12时,为第12个图,白色三角形数为1 2 3 … 11=66个.
14、答案:61,不能
分析:每一次剪完,都比上一次增加6块.第10次剪完后共有纸片6×9 7=61块;2010 -7=2003,2003不是6的整数倍,所以不能剪成。
15、答案:351
分析:张杰:27,29,31,…,77
王强:26,27,28,…,51
差:1,2,3,…,26
共相差:1 2 3 … 26一(1 26)×26÷2—351。
16、答案:120
分析:相邻两项差分别为3、6、10,15、…,会发现这些差相邻两项相差的数为3、4、5、…… 所以第8个数为1 3 6 10 15 21 28 36 =120.
17、答案:72
分析:减去两端的两个人后,刚好每张桌子有两个人:(146-2)÷2—72张。
18、答案:22
如果输入1 3 5,在计算机中显示的结果是1 (1 2 3) (1 2 3 4 5)=22.
19、答案:597
分析:根据题意列出算式为:
2003-215 212 - 215 212 - 215 212 -…- 215 212 - 215—2003 -( 215 - 212) - (215-212) -…- (215 -212) – 215。即前面每次减去3,最后一次减去215.减去215的个数为(2003-215)÷3 1=597(个)
20、答案:2500
分析:原式=1 [(1 2 3)-(1 2)] [(1 2 3 4 5)-(1 2 3 4)] ... [(1 2 3 ... 99)-(1 2 3 ... 98)]
=1 3 5 ... 99
=2500.
21、答案:6
不难发现此图中的数字从左上角开始,按照顺时针方向旋转向内,依次是1、2、3、4、5循环出现,所以☆=1、※=2、△=3,其和为1 2 3=6。
22、答案:15 68
分析:观察这组式子可知两个加数分别由两组等差数列组成,且和也为等差数列
第一组:4,5,6,7,……公差1;
第二组:2,8,14,20,……公差6;
各组和:6,13,20,27,……公差7;
因此,当和为83时,可求得项数为(83-6)÷7 1=12,所以第12项的算式为:
[4 (12-1)×1] [2 (12—1)×6] =15 68.
23、答案:34
分析:通过图观察得到:每个图正方形的个数恰好是层数的平方;36个正方形图形中有6层,除第一个图形外,后而的图形中每增加一层,周长较前面图形周长增加6厘米,形成一个公差为6的等差数列:10,16,22,28,34.所以,图形为36个正方形的周长34厘米.
24、答案:12027
分析:依题意得每组算式的和分别为:3、9、15、21、27、33、39,……由此可知,该组算式的和组成一个首项为3、公差为6的等差数列,则第2005个算式的和为:3 (2005-1)×6=12027.
25、答案:1668
分析:等式左边的加数顺序排列起来就是从2开始的连续偶数,前9个等式左边的加数的个数是3 4 5 6 7 8 9 10 11=63(个),所以第10个等式左边的第一个数是 (63十1)×2=128,最后一个数是(63 12)×2=150,等式右边的和即等式左边的和,为128 130 ... 148 150=1668.
26、答案:229
分析:第1个图形火柴棒根数:4×1=4
第2个图形火柴棒根数:4×(1 2) 1=13
第3个图形火柴棒根数:4×(1 2 3) 2=26
......
第10个图形火柴棒根数:4×(1 2 3 ... 10) 9=229
注:一般而言,数列图形找规律的题目最后都会回到等差数列的计算上来
27、答案:432
分析:第一层:含三角形6×1=6个
第二层:含三角形6×3=18个
第三层:含三角形6×5=30个
.....
第八层:含三角形6×(1 3 5 7 9 11 13 15)=384个
每层含正方形个数为6个,前8层共含正方形6×8=48个
则铺设整个路面所用的三角形和正方形砖块总数是384 48=432块
28、答案:102
分析:所有火柴棒共有三种方向:“/”、“\”和“—”。
从三个方向分别数,实心大三角形共10层,火柴棒数量(1 2 3 .... 10)×3=165根;里面空心三角形为7层,除了底边意外的火柴都拆掉,为(1 2 3 ... 6)×3=63根,所以
165-63=102根。
29、答案:2 35,995
分析:第一个家数以4为周期变化,第二个加数呈等差数列,18÷4=4....2,1 (18-1)×2=35,
所以第18个算式是2 35,因为第一个加数小于等于4,第二个加数为奇数,所以结果为1992的算式只可能是1 1991或者3 1989,如果第二个加数是1991,那么这是第(1991 1)÷2=996个算式,996÷4=249,那么第一个加数应该是4,如果第二个加数是1989,那么这是第(1989 1)÷2=995,995÷4=248...3,第一个加数的确是3,所以第995个算式的结果是1992.
30、答案:18
分析:整个过程中一共转了1 2 3 4 ..... 36=666人次,每转过72人次所有学生的朝向就会和原来一样,那么666÷72=9.....18,于是应该有18名同学面朝外,18名同学面朝里。