图(Graph)是由顶点(Vertex)的有穷非空集合和顶点之间边(Edge)的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
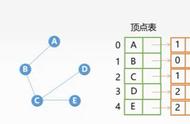
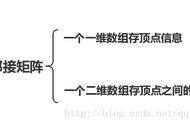
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。
用一个顺序表来存储顶点信息
用邻接矩阵(二维数组)表示顶点间的相邻关系
图按照有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
图上的边或弧带有权则称为网。
在一个图中,每条边或弧可以拥有一个与之相关的数值,我们将它称为权。这些权可以具有一定的含义,比如,表示一个顶点到达另一个顶点的距离、所花费的时间、线路的造价等等。这种带权的图通常被称作网。
图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复的叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称为强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称为强连通分量。
无向图中连通且n个顶点n-1条边称为生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
对于图来说,邻接矩阵是不错的一种图存储结构,但是我们也发现,对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费的。因此我们考虑另外一种存储结构方式:邻接表(Adjacency List),即数组与链表相结合的存储方法。
顶点用一个一维数组存储,另外,在顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图称为顶点vi作为弧尾的出边表。
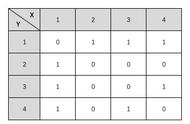
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

图的邻接矩阵的存储结构定义如下:
#define MVNum 50 //最大顶点数
typedef struct{
VertexType vexs[MVNum];
Adjmatrix arcs[MVNum[MVNum];
}MGraph
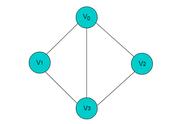
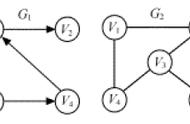
下图是一个4个顶点的无向图:
无权无向图的邻接矩阵可定义为:


下图是一个4个顶点的有向图: