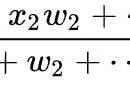1．重力的产生

重力是由于地球的吸引而产生的力，施力物体是地球。在地球表面附近的任何物体都受重力。

2．重力的大小

(1)同一地点，不同物体的重力大小与其质量成正比。即G＝mg，其中g是自由落体加速度。g的单位既可以是N/kg，又可以是m/s2，而且1 N/kg＝1 m/s2(在第四章我们将会证明这两个单位是相同的)。

(2)纬度越高，g值越大，同一物体所受重力越大；海拔越高，g值越小，同一物体所受重力越小。

(3)重力的大小与物体的运动状态无关，与物体是否受其他力无关。

3．重力的方向

重力的方向总是竖直向下，竖直向下不是垂直于支撑面向下，也不是指向地心。

4．重力的作用点——重心

(1)重心是重力的等效作用点，并非物体的全部重力都作用于重心。

(2)重心的位置

①重心的位置可以在物体上，也可以在物体外。例如一个圆形平板的重心在板上，而一个铜环的重心不在环上。

②质量分布均匀、形状规则的物体的重心在其几何中心上；对形状不规则的物体，可以应用二力平衡的知识通过支撑法或悬挂法来确定其重心位置。

③重心的位置跟物体的位置、放置状态及运动状态无关，但跟物体的形状及物体内质量的分布有关。

5．力的图示与力的示意图

注意：有时箭头表示力的作用点。

理解重力和重心时的注意事项

(1)重力是物体由于地球的吸引而受到的力，但并不是地球的吸引力。重力G＝mg，故其大小只与m、g有关，方向与g相同，总是竖直向下。

(2)重心不是重力的真实作用点，重力的作用点遍布整个物体，只是为了研究问题的方便，把物体所受的重力看成都集中在重心这一点。重心的位置与物体的形状和质量分布情况有关，但并不一定在物体上。