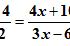等式分类用等号(=)把表示数的两个字符串(包括字符)连接起来的字符串,称为等式。等式分为两类。一,特称命题,等式两端之值存在不等结果。称该等式为非恒等式。二,全称命题,等式两端之值不可能出现不等的结果。这样的等式称为恒等式。上述两个命题,在同范围内,是对立命题。既不能同真,也不能同假。非恒等式还可分为两类。例1,x+1=3,例2,0x+l=3。 例1类,称为有解方程,解为 x=2。 例2类,称为无解方程。不论x取何值等式陈述的相等关系都不可能立。可简写成等式 1=3。 1=3,从整体看,就是一个等式。非恒等式,就是方程式。 小学一年级,学过加法之后,就可引入恒等式与非恒等式概念。3+4,作为一个字符串,给它一个名称,表达式。既示加法运算,又表示相加之后的和数。更具体点,称为二项式。3+4-5称为三项式。.......。通称多项式。(在此,消除了算术与代数之界限)
字符等号“=”把两个表达式连接起来,构成-个新字符串,称此字符串为等式。 一,3+4=7, 二,3+4=6。 都是等式。分为两类。 一,之一类,称为恒等式。 二,之一类,称为非恒等式。等号陈述的相等关系不成立的等式。在引入表示变数或未知数的字符之后。再如前述,就可去创建方程式概念了。有了恒等式的概念之后。当一个表达式作为字符串,形状变化之后,就可与原形式一同构成一个等式。当这个等式是恒等式时,就称这两表达式之一恒等变形为另一表达式。恒等式是已知条件。恒等式两端的表达式不全同时,就称其中一个恒等变形为另一个。 混合运算构成的表达式的恒等变形法则 一个表示数字的数字符,恒等于它与1的乘积。也可认为是一个表达式中的单项式。一个单项式用括号括起来,就是一个数。也是多项式中的一项。当规定,先乘除后加减之后,这对括号就可省略
。当括号内是多顶式时,括号不能省略,要按取消括号的法则进行。逆过来,也一样,不能随意添加括号,需按法则进行。全由数字符中的常数构成的表达式,所表达之数。按下列顺序进行运算。先算括号内之运算。从最内层一对括号内开始运算。每对括号内,都是一个无括号多项式。无括号多项式的运算顺序,先算各单项式,传统说法“先乘除,后加减”。再从左向右依次计算各加减运算。所得结果,规定为此表达式所表示的数。其他变形后的计算结果,与此数比较,相等,则是恒等变形。不相等,则不是恒等变形。恒等变形是一个表达式变形之后来说的。不是对等式变形来说的。对等式,许可的变形,称为同解变形。对于一个恒等式,需要许可变形之后还是恒等式,才是恒等式的同解变形。两端表达式,对表达式同做某非恒等变形,变形之后,还是恒等式,这种变形,对恒等式来说,就是同解变形。等式变形之后,下列许可的变形,才称为等式的同解变形。等式每一端分别进行了恒等变形,对等式来说,也进行了变形。这类变形,对该等式来说,肯定是同解变形。等式两端同加一个数,或同乘除一个非零数。也是同解变形。
表达式之恒等变形。一个表达式的恒等变形法则,分成三个法则来陈述:
,单项式之恒等变形法则,只有乘除构成之表达式的恒等变形法则。1,改变因数位置之法则。首个因数不动,其他因数可联同数字前的乘除号,作为一个整体移动。是恒等变形。2,首项与乘号后的数字交换,是恒等变形。3,改变运算顺序之恒等变形法则。先加括号再算括号内之表达式。加括号时,1,恢复省略之括号。即左括号加在最左侧。右括号可加在任意因数之后。括号内的运算符号保持原样。2,非恢复省略括号时,括号前是乘号,则括号内保持原样;括号前是除号,则括号内之运算符全换成逆运算的运算符。
,a×b÷c÷d×e恒等变形如下: a×b÷c÷d×e =(a×b÷c)÷d×e =(a×b÷c÷d)×e =e×b÷c÷d×a =a÷c×b×e÷d a×b÷c÷d×e=a×b÷(c×d÷e) =a×b÷(c×d)×e=a÷c×b×e÷d==a÷(c÷b÷e)÷d
二,多项式之恒等变形法则。′1,改变单项位置之法则。首个单项不动,其他单项可联同数字前的加减号,作为一个整体移动。是恒等变形。2,首项与加号后的数字交换,是恒等变形。3,改变运算顺序之恒等变形法则。先加括号再算括号内之表达式。加括号时,1,恢复省略之括号。即左括号加在最左侧。右括号可加在任意因数之后。2,非恢复省略时,括号前是加号,则括号内保持原样;括号前是减号,则括号内之运算符全换成逆运算的运算符
,a+b-c-d+e恒等变形如下:a+b-c-d+e =(a+b-c)-d+e =(a+b-c-d)+e =e+b-c-d+a =a-c+b+e-d a+b-c-d+e=a+b-(c+d-e) =a+b-(c+d)+e=a-c+b+e-d==a-(c-b-e
三,分配律作用下之恒等变形分配律为根据之恒等变形。既含二级运算
的一段多项式的恒等变形。一般形式。α x b ± a x c = a x (b ± c)=(b ± c) x ab ÷ a ± c ÷ a= (b ± c) ÷ a都是恒等变形。
a÷b±a÷c=a÷(b±c)不是恒等变形!