统计分析的目的:
- 收集数据,整理分析数据和由数据得出的结论的一组概念、原则和方法。
- 描述性统计,利用表格、图形或者数值来展示数据中的信息。
- 推断性统计,利用样本获得的数据对总体的性质进行估计或检验,总体的性质通常使用概率模型来刻画。
对历史数据的分析,总结及解释历史规律,然后是基于历史数据得出的模型对未来作出预测。
统计分析的关键概念:
- 测量尺度,名义尺度、顺序尺度、间隔尺度、比例尺度,可以进行频数分布。定类尺度,对数据进行分类,常见的性别、地区、学历等。定序尺度,变量类型除了分类作用之外外可以实现排序,比如排名,意愿度等。定距尺度,可以进行分类、排序、加减,没有绝对零点,如温度,常用分析方法,频数的分布,平均值,标准差等。定比尺度,分类、排序、加减、乘除数值型的变量,可以进行运算,可以使用频数分布、均值、标准差等。通常将定类与定序数据合称为分类变量通常使用频次统计,将定距与定比合称为连续变量可以使用描述统计方法。
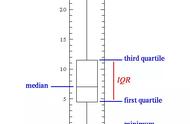
- 几种趋势,均值、中位数、众数
- 离散趋势,频数分布、标准差、方差、四分位差、百分位数、极差、离差平方和、离散系数。
均值:
- 通常所说的均值指的是算术平均值,算术平均值=数据的合计÷数据的个数
- 几何平均,几个平均是n个数字的乘积的n次方根的正数值,只有数据为正数时才可以计算。

- 调和平均值,把n个数字的倒数的和作为分母,把n作为分子的值,只有在数据为正值时才能计算。调和平均=数据的个数÷数据的倒数的和,可能使用场景在较多数据值集中在最小值附近。
- 调整平均值,是指从上限值和下限值去掉一定比例的数据后剩下的数据的算术平均。
使用相同的数据进行计算的结果,算术平均、几何平均、调和平均、依次是由大到小地变化或者相等。
中位数:
是指把数据由大到小排列时居于中间的值。
比如在年收入的集中趋势时,因为少数人的收入金额非常的巨大,导致整体的均值也会很大,此时中位数可能会更好地反映整体情况。
众数:指在数据分布中出现最多项的数值。通常通过频数分布表示。
极差和标准差
对数据的离散状态进行确认,分布大,在集中趋势周围广泛地分布着各种数据。分布小,数据是密集的,差异小的,所以分布大小的代表性指标就有标准差和极差。
极差,值分布的最大值和最小值的距离,极差的性质随样本量的变化而变化,即使相同的抽样总体中抽取样本,一般来说,极差在样本量多的时候要比样本量小的时候大,比较2个以上组的极差时,要力求各组样本量相等。
标准差,表示各个数据相对均值的离散程度,数据的平均值与各个数据的差的平方的平均值以及这个平均值的方根,差的平方的平均值叫做方差,平均值的平方根叫做标准差。标准差的计算中有的除以n,有的除以n-1,当计算总体的标准差时除以n,在计算抽样样本时标准差除以n-1,原因是人为增大标准差,提高样本代表性。