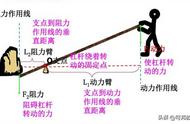
(2016节选)如图所示，由不同物质制成的甲和乙两种实心球的体积相等，此时杠杆平衡(杠杆自重、挂盘和细线的质量忽略不计)。则杠杆左、右两边的力臂之比为__________，1个甲球和1个乙球的质量之比为__________，甲球和乙球的密度之比为__________。

答案：2∶1　1∶3　1∶3　

答案解析：左右两个挂盘的拉力竖直向下作用在杠杆上，力臂刚好落在杠杆上，从图中可以以看出左边的力臂是四格，右边的力臂是两格，则力臂之比是2：1。这道题是一道典型的杠杆问题，应该要用杠杆的平衡条件来解题。杠杆左右两个挂盘对杠杆的拉力等于挂盘里面物体的总重力，左边是两个甲加上一个乙，右边是一个甲加上三个乙。根据杠杆平衡条件得F1L1=F2L2，即（2G甲 G乙）*4=（G甲 3G乙）*2，整理之后得到G甲：G乙=1：3，G=mg，g是定值，则m甲：m乙= G甲：G乙=1：3。甲、乙两球体积相等，即V甲=V乙，由密度公式ρ＝m/V可代入具体数值算出甲、乙的密度，从而得到密度之比是1：3。（具体可见前面的比值问题的计算）

牛刀小试：

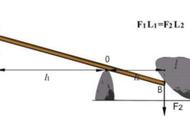
(2018节选)如图所示是建筑工地上的起重机的示意图。起重机的电动机功率为3×103 W，当它把质量为1 t的重物匀速提起24 m时，用时100 s。(g取10 N/kg)若起重机上AB长为20 m，吊起重物时B端的配重质量为4 t，为使起重机不翻倒，则OB长为多少？(不计摩擦和起重机自重)