四年级数学下册各单元知识要点

第一单元《四则运算》

知识点1：没有括号的同级运算。

在没有括号的算式里，如果只有加、减法或乘、除法运算，要按照从左到右的顺序计算。

计算加减混合运算，有时为了计算简便，可以适当调整算式中运算的顺序，要把题中的某数带着数前的运算符号“搬家”。

213 48－13

=213－13 48 【学生容易写成

=200 48 213 13－48】

=248

72×36÷8

=72÷8×36【学生容易写成

=9×36 72×8÷36 】

=324

易错题： 15÷5×3 25×3÷25×3

=15÷15 =75÷75

=1 =1

这两道题是没有掌握好同级运算的顺序，认为怎样好算就怎样算。

知识点2：没有括号的四则混合运算。

在没有括号的算式里，有乘、除法和加、减法，要先算乘、除法，后算加、减法。

易错题：75 25÷5 134－34÷34 66

=100÷5 =100÷100

=20 =1

这两道题还是没有掌握好四则混合运算的顺序，算式中有乘除法和加减法，要先算乘除法，后算加减法。学生认为怎样好算怎样算。

知识点3：带括号的四则混合运算。

含有小括号的混合运算，要先算括号里面的，再算括号外面的。

知识点4：运用混合运算解决问题。

分析、弄清题中的条件与问题的关系，其实就是解决应用题常见的一种方法——分析法。它是从应用题要求的未知数入手，根据数量关系，找出解答最后结果所需条件，把其中的一个或两个未知条件作为要解的问题，然后找出解决这一个或两个问题所需要的条件，这样逐步逆推，直到所找的条件在应用题中都是已知的为止。

易错题：张师傅要生产600个零件，已经生产了120个，剩下的要10天完成，平均每天生产多少个？

600－120÷10

=480÷10 （学生知道应先算减法，但总忘加括号）

=48（个）

解题时要弄清数量之间的关系与先后顺序，如果要先算第一级运算，一定要在第一级运算上加上小括号。

第二单元《位置与方向》

知识点1：确定物体位置的条件。

方向和距离，两个条件缺一不可。

知识点2：在平面图上标出物体位置的方法。

先确定方向，在确定距离，最后画出物体具体位置，并标明名称。确定方向时选择与物体所在离得较近（夹角较小）的方位；距离必须以选定的单位长度为基准来确定。

巧计：物体位置要想找，方向、距离缺不了。

方向确定在找角，一般选小是首要。

距离大小有参数，下方标注不可少。

易错题：①如图，A点是学校的教学楼，B点是体育馆，则体育馆在教学楼的北偏西30⁰方向上。

此题错在对教学楼的具体方向的叙述不清楚。 30⁰角是由正西方向偏向北得到的，所以叙述时应先说西方，再说北方。

正确答案为：体育馆在教学楼的西偏北 30⁰方向上。

在叙述物体的方向时，一般先说与物体所在方向离得较近（夹角较小）的方位。

②小明家在小东家南偏西40 ⁰ 方向500米处，画平面图表示小明家的位置如下：

此题错误有两处：一是观测点确定不对，应以小东家为观测点画方向标；二是单位长度不统一，小明家到小东家的距离应以图标为准，画出5个等长的 。

技巧：画平面图时，首先要确定好观测点，其次确定被观测物体的方向，最后以选定的单位长度为基准来确定距离。

知识点3：物体位置的相对性。

叙述物体的位置时，要考虑物体位置的相对性，如何叙述物体的位置与观察点有关，观测点不同，物体位置的叙述就不同。

易错题：①甲地在乙地的东偏北30⁰方向900米处，也可以说乙地在甲地的西偏南60⁰方向900米处。

此题错在对位置的相对性理解不好，对角的度量知识掌握不扎实。

画图理解更直观：

正确解答为甲地在乙地的东偏北30 ⁰ 方向900米处，也可以说乙地在甲地的西偏南30 ⁰ 方向900米处.

技巧： 两地的位置具有相对性，以这两个不同地点为观测点描述对方所在地的方向时，方向正好相反（东→西，北→南，东偏北→西偏南）。

②画出活动中心与幼儿园的位置。

A活动中心在广场的西偏北20 ⁰ 方向50米处。

B幼儿园在活动中心的南偏东40 ⁰ 方向100米处。

此题错在审题不认真。幼儿园的位置是相对于活动中心而说的，就应以活动中心为观测点建立方向标来确定幼儿园的位置。切忌确定物体的位置，观测点一定要找准。

知识点4：描述路线图的方法。

按行驶路线，先确定观测点及行走的方向和路程再描述。

第三单元《运算定律与简便运算》

知识点1：加法运算定律。（加法交换律和加法结合律）

加法交换律：两个加数交换位置，和不变。即a b=b a

加法结合律：先把前两个数相加，或者先把后两个数相加，和不变。即(a b) c= a (b c)

技巧：在一个加法算式中，当某些加数可凑成整十数或整百数时，运用加法交换律、加法结合律来改变运算顺序，可以使计算简便。

易错题： 182 765 108

=182 108 765

=300 765 【计算失误，182与108的和不是300】

=1065

技巧：在进行加法简便计算时，有时两个数相加未必能凑成整百数，只能凑成整十数，因此要认真观察，准确计算。

24 127 476 573

=24 476 127 573 【（24 476） （127 573）】

=500 700

=1200

此题错在没有真正理解加法的运算定律，运用加法结合律时要注意把结合的两个数用括号括起来。

加法运算定律的灵活运用：

计算256 249 251 246

=250 6 250－1 250 1 250－4

=250×4 （6－1 1－4）

=1000 2

=1002

技巧：当几个数相加，加数都比较接近某一个数时，可以把这个数作为基准数，看看有多少个这样的基准数，然后加上或减去比基准数多或少的数，求出结果。这种方法简称基准数加法。

知识点2：乘法运算定律。（乘法交换律、乘法结合律和乘法分配律）

乘法交换律：交换两个因数的位置，积不变。a×b=b×a

乘法结合律：先乘前两个数，或者先乘后两个数，积不变。

即(a×b)×c= a×(b×c)

乘法分配律：两个数的和与一个数相乘，可以把它们与这个数分别相乘，再相加。或两个数的差与一个数相乘，可以把它们与这个数分别相乘，再把所得的积相减。

即(a±b)×c= a×c±b×c或a×（b±c）= a×b±a×c

（多个数的和或差与一个数相乘，可以把这些数分别与这个数相乘，再相加或相减。即(a±b±c)×m= a×m±b×m±c×m）

易错题： 50×(4×5)

=50×4 50×5【混淆了乘法结合律与乘法分配律】

=200 250

=450

技巧： 只有运用运算定律能使运算简便时，才能运用运算定律，否则直接按四则混合运算顺序计算。乘法结合律与乘法分配律的最大区别是乘法分配律必须在乘、加或乘、减两种运算中进行。

76×101

=76×100 1【没有正确理解乘法分配律，76×101可以想成=7600 1 是101个76，也就是100个76与1个76的和。】

=7601

15×21 15×78 15

=15×（21 78） 15【虽然计算结果正确，但在简算过程中没

=15×99 15

有把第三项“15”看成“15×1”参与=1485 15 到计算中，而导致计算不是最简便。】

=1500

技巧： 正确理解乘法分配律是运用好乘法分配律的前提。运用简便算法计算时，一定要仔细观看算式结构及数的特点，有时需将一个数转化成两数乘积的形式再进行简便计算。

乘法运算定律的灵活运用：

计算25×32×125

=25×（4×8）×125

=（25×4）×（8×125）

=100×1000

=100000

技巧： 在乘法计算中，也有“凑整”的计算。如：2×5=10,25×4=100,125×8=1000.因此计算连乘算式时，当有的因数不具备“凑整”条件时，可以运用分解的方法，把一个因数分解为两个因数相乘的形式，是其中的因数与其他数的乘积“凑整”，这样会使计算更简便。

知识点3：连减的简便计算。

减法性质：

①一个数连续减去两个减数，可以用这个数去这两个减数的和，即a－b－c=a－(b c)。

②在连减运算中，任意交换减数的位置，差不变。

即a－b－c= a－c－b。

注意： 括号前面是加号，去掉括号，原括号内运算符号不改变；加号后面添括号，括号里面原运算符号不变号；括号前面是减号，去掉括号，原括号内运算符号要变号；即a－（b－c）=a－b c；减号后面添括号，括号里面原运算符号要变号即a－b c= a－（b－c）。

易错题： 596－48 52

=596－100 【此题错在审题不认真，只看数据能否凑整，

=496 而忽略了算式的整体性。】

技巧： 加、减混合运算中，要想交换数的位置，一定要连同前面的运算符号一同交换；加括号时，如果括号前面是加号，括号里面不变号，如果括号前面是减号，括号里面要变号。

762－598

=762－600－2 【没有真理解“凑整”的意义，把598看成600 =162－2 时，已经多减去一个2，就应加上一个2.】

=160

技巧： 在加法或减法计算中，当某个数接近整十、整百、整千时，可以把这个数当成整十、整百、整千的数进行加、减，对于原数与整十、整百、整千相差的数，要根据“多加要减去，少加还要加，多减要加上，少减还要减”的原则进行处理。

知识点4：连除的简便计算。

除法的性质：

①一个数连续除以两个数，可以用这个数除以两个除数的积，即a÷b÷c=a÷(b×c)。

②一个数连续除以几个数，任意交换除数的位置，商不变，即a÷b÷c÷d=a÷c÷b÷d= a÷d÷b÷c。

在一个除加、除减的算式中，当除数相同时，可以运用a÷c±b÷c =(a±b)÷c使运算简便。

易错题： 500÷25×4

=500÷100 【错在随便改变运算顺序，导致计算结果错误】

=5

技巧： 当乘除混合运算中不具备简算因素时，应按照从左到右的顺序计算。

解题口诀：

一看：看数的特点；

二想：想运用什么运算定律；

三做：再进行计算；

四查：检查是否正确。

第四单元《小数的意义和性质》

知识点1：小数的意义和小数的计数单位。

小数的意义：分母是10、100、1000……的分数可以用小数表示。小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……每相邻两个计数单位间的进率是10.

易错题：

①小数都比1（整数）小。

此题错在对小数认识不够，小数点的左边可以是任意的整数。没有最大的小数，也没有最小的小数。

② 0.35里面有5个0.01.

此题错在对小数的意义理解不到位，因为小数是分数的另一种表示形式，所以将小数变成分数，更容易理解其意义。

③ 最大的一位小数是0.9.

此题错在对一位小数的概念认识不清。所谓一位小数，是指小数部分是一位的小数，而整数部分可以是任意的数。比如：10.9、100.9、999.9……都是一位小数。没有最大的一位小数，最小的一位小数是0.1.

知识点2：小数的读写法。

小数的读法： 先读整数部分，按整数的读法读；再度小数点，小数点读作“点”；最后读小数部分，依次读出小数部分每一位上的数字。

小数的写法： 先写整数部分，按照整数的写法去写，如果整数部分是零，就直接写“0”；再在个位的右下角点上小数点；最后依次写出小数部分每一个数为上的数字。

注意： 读数时要写中国小写数字（语文的字），写数时要写阿拉伯数字，读小数部分时，一定要注意所有的“0”都要一一读出。

知识点3：小数的性质和小数的大小比较。

小数的性质：小数的末尾添上“0”或去掉“0”，小数的大小不变。

小数大小比较方法：先比较整数部分，整数部分大的那个数就大；整数部分相同的，十分位上的数大的那个数就大；十分位上的数也相同的，百分位上的数大的那个数就大……

易错题：

① 0.2和0.20大小相等，意义相同。

此题错在对小鼠的意义认识不清。0.2的计数单位是1／10，表示2个0.1，而0.20的计数单位是1／100，表示20个0.01，因此0.2和0.20表示的意义不同。小数的末尾添上“0”或去掉“0”，虽然不改变小数的大小，但计数单位却发生了变化。

② 大于5且小于6的小数只有9个。

此题错在缩小了小数的取值范围。如果以1／10为计数单位，则5.1～5.9都是大于且小于6的一位小数；如果以1／100为计数单位，则5.01～5.99都是大于且小于6的两位小数；以此类推，如果没有小数数位的界定，大于5且小于6的小数应有无数个。切记两个整数间的小数有无数个。

知识点4：小数点移动引起小数大小变化的规律及应用。

小数点移动引起小数大小变化的规律：小数点向右移动一位，小数就扩大到原数的10倍；移动两位，小数就扩大到原数的100倍，移动三位，小数就扩大到原数的1000倍……反之，小数点向左移动一位，小数就缩小到原数的1／10；移动两位，小数就缩小到原数的1／100，移动三位，小数就缩小到原数的1／1000……

小数点移动引起小数大小变化的规律的应用：把一个数扩大到它的10倍、100倍、1000倍、……就是用这个数分别乘10、100、1000……

小数点就要相应的向右移动一位、两位、三位……把一个小数缩小到它的1／10、1／100、1／1000……就是把这个数分别除以10、100、1000……小数点就要相应的向左移动一位、两位、三位……

注意： 小数点向右移动时，整数部分最高位前面的0必须去掉（0.3）；如果小数部分不够，要在右边添“0”补足数位。要数清移动的位数

知识点5：名数的改写。

注意： 在改写60千克=( )吨时，不要写成0.6吨，应是0.06吨。还有面积单改写易错，如5平方米=（ ）平方分米，错写成50平方分米，进率是100. 应是500平方分米。

知识点6：求一个小数的近似数。

求小数近似数的方法：求小数近似数可以用“四舍五入法”。当保留整数时，表示精确到个位，应根据十分位上数字的大小来判断是否进位；保留一位小数时，表示精确到十分位，应根据百分位上数字的大小来判断是否进位；保留两位小数时，表示精确到百分位，应根据千分位上数字的大小来判断是否进位……

把不是整万或整亿的数改写成用“万”或“亿”作单位的数的方法：

先确定万位或亿位，然后在万位或亿位的右下角点上小数点，最后在小数的后面加上“万”字或“亿”字，如果小数的末尾有0要去掉，改写后还可以根据要求保留小数。

注意：保留几位小数，只要看保留小数位数的下一位，后面无论有多少位数，都不用考虑。求近似数时，一定要用“≈”连接；改写成用“万”或“亿”作单位的数时，位数不够，在前面添“0”补足。

第五单元《三角形》

知识点1：三角形的定义与特性。

三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连）角做三角形。从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形具有稳定性。

易错题：直角三角形只有一条高。

此题错在没有认识到直角三角形的两条直角边也是直角三角形的高。任意一个三角形都有三条高。

还有画高时，一定要保证垂线和底边相交所成的角是直角。

知识点2：三角形的三遍的关系。

三角形任意两边的和大于第三边。

判断三条线段是否能围成三角形，只要把最短的两条边相加与最长变比较即可。如果最短的两条边之和大于第三边，也就证明任意两条边之和大于第三边。

知识点3：三角形的分类。

三角形按角分为：锐角三角形、直角三角形和钝角三角形。因为在一个三角形中至少有两个锐角，所以可以根据最大的角判断三角形的类型。最大的角是哪类角，它就属于那类三角形。

三角形按边分为：不等边三角形和等腰三角形，等腰三角形包括等边三角形。

易错题：等腰三角形一定是锐角三角形。

此题错在对等腰三角形概念理解模糊。两边相等的三角形就是等腰三角形，它与角的大小无关。在直角三角形和钝角三角形中，如果有两条边相等，也可以称其为等腰三角形。等腰三角形可以是锐角三角形、直角三角形和钝角三角形。

知识点4：三角形的内角和。

知道三角形内角和是180⁰.并会根据要求求其它角。

易错题：判断一个三角形中最多有两个直角。（√）

此题错在不会应用三角形内角和180⁰来分析问题。一个三角形中最多有一个直角。

知识点5：图形的拼组。

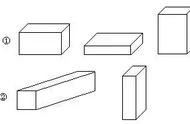
任意两个相同的三角形都可以拼成一个平行四边形；两个相同的直角三角形可以拼成一个长方形或平行四边形；两个相同的等腰直角三角形可以拼成一个正方形或平行四边形；三个相同的三角形可以拼成梯形。

易错题：①只有完全相同的两个三角形才可以拼成四边形。

此题错在不清楚三角形拼摆四边形的条件。当两个三角形有一条边相等时，这两个三角形就可以拼成四边形。而只有完全相同的两个三角形才可以拼成一个平行四边形。

②两个相同的直角三角形一定能拼成一个正方形。

此题错在结论过于绝对化，当直角三角形的两条直角边不相等时，拼成的四边形只能是长方形。

两个相同的直角三角形（非等腰）可以一拼成一个长方形。

第六单元《小数的加法和减法》

知识点1：小数的加、减法。

笔算小数加、减法要注意：

1.计算小数加、减法时，要注意小数点对齐，也就是把相同数位对齐。

2.从低位算起，按整数加、法进行计算，得数对齐小数点的位置，点上小数点。

3.得数（指小数）的末尾有0，一般要去掉。

易错题： 16.5－13.81=2.71

16.5 【错在减数百分位上的1 不应落下来，而应－13.81 把被减数16.5看成16.50再计算。】 2.71

技巧：在笔算小数减法时，当小数位数不同时，可以根据小数的性质在小数末尾添上0，使两个小数数位相同后再相减。还要看清运算符号后再计算。

知识点2：小数的四则混合运算。

小数加减混合运算的运算顺序同整数加减混合运算顺序相同。

易错题： 35.65－（18.65 4.15）

=35.65－18.65 4.15【去括号没有改变括号内的运算符号】

=17 4.15

=21.15

技巧：此题可用减法性质1的逆运算来解决，还可以运用整数运算中去括号的方法解决。

27.24 18.6－20.3

=29.1－20.3 【错在相同数位没对齐，百分位上的4要落下来，十分位上的2应与6相加。】

=8.8

知识点3：小数加减法的简便运算。

整数的运算定律在小数运算中同样适用。

易错题： ① 5.84 4.16－5.84 4.16

=（5.84 4.16）－（5.84 4.16）

=10－10 【审题不认真，只看数据的特点，却忽略了数 与数之间的关系及每个数前面的运算符号】

=0

技巧：小数加减混合运算中，要想交换数的位置，一定要连同数前面的运算符号一同交换。

②15.46－5.7 4.3

=15.46－(5.7 4.3)

=15.46－10 【此题只考虑数据能否凑整，而忽略了简算是否可行。】

=5.46

技巧：简算时如果需要加括号，一定要注意变号规则：如果在加 号后加括号，括号里面不变号；如果在减号后加括号，括号里面要变号。

第七单元《统计》

知识点1：折线统计图的画法及折线统计图的特点。

折线统计图的特点：既可以反映数量的多少，又能反映数量的增减变化。在实际问题中，如果需要了解数量增减变化，选用折线统计图比较合适。

画折线统计图的步骤：①描点；②连点成线段；③标明数据。描点时应注意先找准横轴上的点，在找准纵轴上相对应的点，过两点画横轴、纵轴的垂线，两条垂线的交点便是所要描的点。

注意：①描点时一定要关注所描点的位置与纵轴上的数据是否对应。②如果所选统计的一组数据比较大时，可选择最小的数据为基础数，0至基础数这一段用折线表示。③绘制时要根据实际问题中的数据特点来确定绘制什么样的统计图。一般情况下，条形统计图可以表示数据的多少，折线统计图不仅表示数据的多少，还表示数据增减变化的情况。

知识点2：运用折线统计图进行数据的分析和数据的预测。

可以根据统计图发现问题、解决问题并进行简单的预测。

第八单元《数学广角》

知识点1：关于一条线段且两端植树的问题：指数的棵树=间隔数 1。

知识点2：关于一条线段且两端不植树的问题：指数的棵树=间隔数－1。

知识点3：关于一个封闭图形的植树问题：指数的棵树=间隔数。

封闭图形的周长 =间隔数×株树。 较复杂的应用题从问题入手进行分析更有助于问题的解决。