“三线合一”这个重要性质一般是用全等三角形来证明,但咱们还没讲到全等三角形。我就说个更直观更快速的证明:因为等腰三角形是对称图形,并且角平分线、中线和高都是对称轴,所以它们是同一条线。
由“三线合一”的性质可以推出等边对等角,即如果一个三角形两边长相等,那么底角相等。等边对等角的逆定理等角对等边依然成立。

现在回到原来问题,因为底边长 n 是已知数,想知道三角形面积咱们只需要知道高是多少。
3第一步,做一条高,根据三线合一,这条高同时也是底边的中线;
第二步,用勾股定理算出高。
第三步,底乘高乘二分之一算出三角形面积。
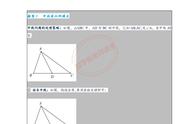
当知道等腰三角形有一个角是60°时,无论已知的60°的角时底角还是顶角,都能推出这个三角形时等边三角形(如下图1,2)。下面我们来分别证明。

如图1,若已知AB=AC,∠B=60°,则由等边对等角推得∠C也等于60°,继而∠A=180°-60°-60°=60°,再由等角对等边,知三边长都相等。
如图2,若已知DE=DF,∠D=60°,则∠E ∠F=180°-60°=120°,又因为∠E=∠F,所以都等于60°,再由等角对等边,知三边长都相等。
以上两个证明虽然不难,但往往是很多学生所缺乏的,他们觉得简单的就不证了,难的又不会证,导致数学学习中缺乏“证明”这项训练。后果是,很多定理公式都不知道怎么来的,于是就只能死记硬背,学习没有效率。
所以说平时看到公式定理,要试着证证,比如图3:一个等边三角形三边长都是 a ,面积公式为什么就是四分之根号三倍的 a 方呢?自己尝试证明吧,知道这个公式能大大提高解题速度。
4等腰三角形有“胖”、“瘦”之分

这个胖和瘦,是我为了直观地说出它的特点而讲的。
数学学习中存在的一个问题就是很多说法“太严谨”了,因为教数学的老师都是自小严谨地学出来的,刚才那句“胖瘦之分”就会被表述成“腰长一定的等腰三角形,顶角的大小决定底边的长度”。
但这样说出来不直观,学生不易记忆。所以我在这个系列正文部分会多讲些形象化的东西,严谨的定理放在“要点回顾”部分。
等腰三角形顶角常见的是这么几个特殊角:60°、90°和120°,这三种顶角对应的底边长可以算出来具体数值。