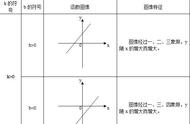
关于二次函数动点问题的解答方法:
⑴ 求二次函数的图象与x轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数ax² bx c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于
对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax² bx c﹙a≠0﹚本身就是所含字母x的二次函数;

二.利用平行或垂直关系求某直线的表达式
1.平行关系-------当两直线平行时,它们的K值会相等或不变;
2.垂直关系-------当两直线垂直时,它们的K值互为负倒数;
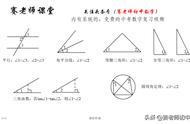
题型解读4 二次函数与特殊三角形的存在性问题
【解题方法】
1.等腰三角形的分类讨论:三条边两两相等分三种情况进行分类讨论,注意结合“三线合一”性质解题(可借助“两圆一线”初步判别答案的个数);
2.直角三角形的分类讨论:以三个直角顶点分三种情况进行分类讨论,注意结合直角三角形的性质解题;
3.等腰直角三角形的分类讨论:先直角再等腰顺序进行分类讨论;
题型解读5 二次函数与三角形全等、相似的存在性问题
【解题思路】
1.利用三角形全等性质进行解题;
2.中文字说相似,首先考虑分类讨论,
①等角确定时,采用代数方法-----“一个固定一个互换”;
②等角不确定时,采用几何方法----利用等角的三角函数值解题;
题型解读6 二次函数与特殊四边形的存在性问题
【解题思路】
1.几何论证方法
思路过程:①画出所有存在的图形(一般以两个已知点所在的线段为平行四边形的短边、长边、对角线为依据去画图);
②运用几何知识;(全等、相似或各图形的几何性质)解题;
③符合题中出现“点的位置特殊或受限制”的情景
2.代数论证方法
思路过程:①写出或表示出已知三点的坐标;两两为对角线分三种情况分类讨论;
②若求第三点坐标-----“特殊四边形专有性质 两点间距离公式或题目条件”列方程求解;
③若求第四点坐标----用“平移法”表示第四点坐标,用“两点间距离公式或题目条件”列方程求解;
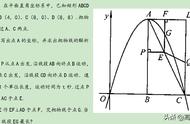
题型解读7 二次函数与周长、面积问题
【解题思路】面积问题,注意首先确定面积方法(五种),再依面积方法展开分析思路推导;
题型解读8 二次函数与定值、最值问题
【解题思路】
①利用二次函数解决:求出解析式,用二次函数配方求最值的方法来解题;
②利用几何性质解决: 垂线段最短、两点间线段最短(转化为同一线段、将军饮马问题)