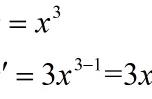在中考数学的二次函数压轴题中，由动点产生的直角三角形问题也是热门考点之一。通常的解法都是在以动点分别向x轴和y轴作垂线，构造我们熟悉的几何模型，例如“一线三等角”后者“8字型”等等。那么对于一些想追求高分的同学，如果能够利用关于垂直问题的几个解析法小技巧，就可以大大加快解题速度，尤其是对于那些题目中要求只写出答案，不用给出解题过程的题目。

【分析】第一问，由一次函数表达式可以确定A、C两点的坐标，然后将其代入二次函数表达式即可。

【分析】对于△PCM为直角三角形这样的条件，正常的思路应该是分为三种情况来考虑，即P、C、M分别为直角顶点情况。本题的点M，为在抛物线上的动点P向x轴做垂线与直线AC相交所得，则∠PMC一定为锐角，那么就只剩下两种情况需要考虑，分别是P为直角顶点和C为直角顶点。

当P为直角顶点时，情况比较简单，就是点P和点C的纵坐标相同时就是所求。

当C为直角顶点时，过C点做直线AC垂线，与抛物线的交点就是P点位置。所以问题的关键在于求出直线PC的表达式，方法有三种：

第一种：利用三角形相似得到对应边成比例，求出直线PC与x轴的交点D的坐标，进而求得直线PC

第二种：利用两条垂直的直线，斜率相乘等于-1，利用直线的点斜式方程，直接写出直线PC的表达式。

第三种：根据P点在抛物线上，直接设出点P坐标，再利用P、C两点求出直线PC斜率的表达式，与直线AC的斜率相乘等于-1，直接确定P点坐标。

这里需要注意的是，“斜率相乘等于-1”、“点斜式方程”和“两点求斜率”属于高中解析几何中直线部分的知识点，初中并未涉及，所以在中考时，如果题目要求写解答过程，这种方法需要慎用。在中考时，部分题目要求直接写出答案的，可以使用上述的第二种和第三种方法来提升做题效率。

建议有能力的同学要在中考之前将这部分的高中知识进行学习，最好熟练应用，一是可以提升在中考时的解题效率；二可以减轻高中学习的压力；三是提前锻炼解析几何处理图形问题的思维，因为上了高中就知道了，初中的平面几何思路基本不用。

本题采用最常规的三角形相似来进行解答。