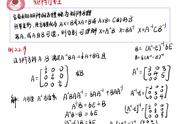如果遇到了公式中没有出现过的新组合，我们同样是有应对的策略的，

因为我们有规律，有理解。规律是什么呢？

1. 行列式的乘法，矩阵的加法都是十分符号常数的运算规律的。

2. 矩阵的转置，求逆，求伴随没有先后之分，既是右上角如果有多个运算时，可以自由的调整这三个运算间的顺序。

3. 整体思想的应用，如果我不知道上一条性质，然后求（A-1）*，我们知道A-1也是一个矩阵，那就把它看作一个整体，直接代入到A*=A-1（A的行列式）这个公式中，就可以得到原式=（A-1）-1（A-1的行列式）=A/（A的行列式）。我们心里应该时刻清楚，哪一个整体还是个矩阵，哪一块是一个常数

4. 对于特殊的题型，我们也可以采用分析的方法，即先用公式做初步的转换，之后根据实际意义分析，举例如下：

我们对原式取行列式就可以分析得到A的行列式的平方=1，结合小于0的条件得出A=-E,所以最终结果是0.

（二），抽象逆矩阵型

这一种乍一看似乎可以用公式解决，但实际上不可以，因为它恰恰属于公式中的“不一定”，类型比较单一，同时也成就了其特殊性，如下图：

（三），行列抽象变换型

这个是上述（五）的抽象版，但是我们不要被其迷惑住，仍然按照刚刚说过的思路来写。举例如下（a1,a2,a3,均为列向量）

很显然，P=(111 123 149)

，而且要注意的是，因为A是列向量，所以要把A放左边。

（四），分块矩阵的行列式型

这里主要是注意不要把分块矩阵当成一个普通的元素了，这里只强调一个算法，就是把左下角消成0，举例如下：