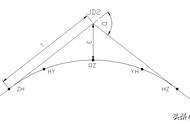
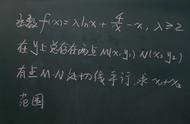设抛物线焦点为F，M为AB中点,O'为△C'AB外心。有以下问题：

24 求满足AC’⊥BC’的点C’的轨迹，AB是否经过定点？

25求证∠FC’A=FBC'，∠FC’B=FAC'，∠C’FB=AFC'，

26 求证△C'FA∼△BFC',

27 求证C'F^2=FB*FA，

28 求证∠FC’A=BC'M，

29以C'O'为直径的圆是否恒过定点？

24 求满足AC’⊥BC’的点C’的轨迹，AB是否经过定点？

思路分析一：

设出切点，得到交点坐标，由切线垂直得到条件即可得到C’在准线上，下面利用准线性质或者上面性质即知切点弦过F。

证明一：

思路分析二：

利用上节焦点弦的性质易知C’在准线上，下面由一一对应证明C’的唯一性即可。

证明二：

设过A的切线交准线于C,弦AB’过F，由上节性质23知C’B’为切线，故B,B’重合。C,C’重合。由上节性质17知∠AC’B=90°，故C’在准线上。又由性质5知切线与切点纵坐标一一对应，故A的切线上只有点C’满足∠AC’B=90°，从而C’的轨迹为准线。

注：

本性质承上启下，既是焦点弦的性质，又和抛物线的两条切线有关。本性质即过抛物线焦点的弦在两交点处的两条切线互相垂直，而且交点在准线上，反之亦然。

此性质也是圆锥曲线共有的性质，对于椭圆轨迹为圆，一般称为蒙日圆或者准圆。可以参照本系列的第五篇(《直线与椭圆位置关系常见问题1—圆锥曲线系列讲义之五》)的问题5。双曲线性质类似，轨迹也是圆。抛物线中此圆退化为准线。相应的抛物线性质的计算量也就小了很多。